浅谈 Uplift Modeling

概览

Uplift 本意为「上升；抬起；提振」，在因果推断中引申为「某种干预对于个体状态或行为的因果效应」。在推荐系统领域中，增益模型（Uplift Model）用于预测「干预后的增量反馈价值」，可以表达为： \[ \mathrm{Lift}=P\left( \mathrm{State}\mid w\,\,\mathrm{Treatment} \right) -P\left( \mathrm{State}\mid w/o\,\,\mathrm{Treatment} \right) \] 增益模型的落地价值体现在「智能化营销」领域，用于衡量和预测营销干预带来的「增量提升」，把营销预算投入在说服型（Persuadables）用户上，不浪费在确认型（Sure Things）和沉睡型（Lost Causes）用户上，避免对勿扰型（Sleeping Dogs）用户产生反效果^[2]：

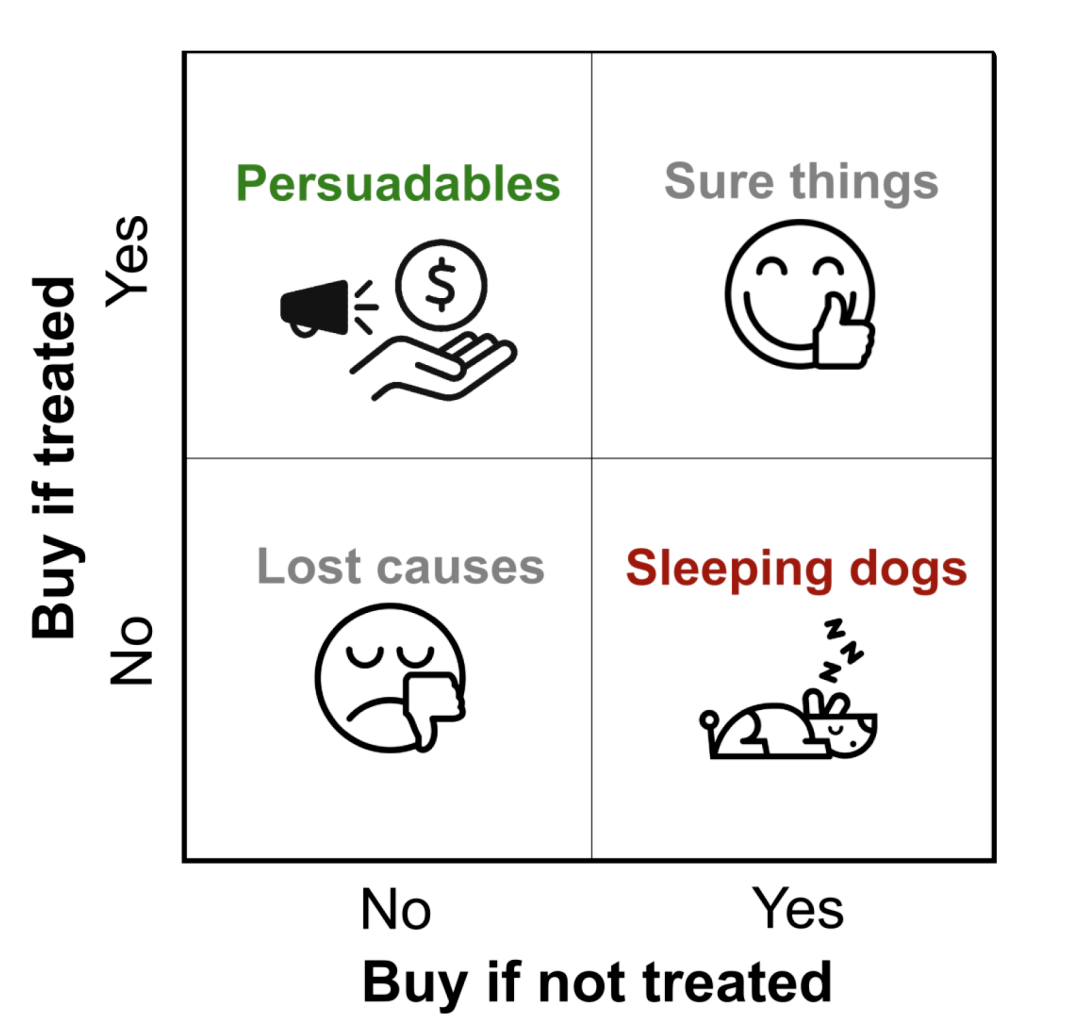
与之对应的是响应模型（Response Model），其目标是预测「干预后的个体状态或行为」，这是一个相关性分析问题（而不是因果推断问题），因此会导致我们无法区别自然转化人群。在营销领域，响应模型可以用于估计用户看过广告后的购买率，但增益模型是估计用户因为广告而购买的概率，帮助精准寻找营销敏感人群。响应模型可以表达为： \[ \mathrm{Outcome}=P\left( \mathrm{State}\mid w\,\,\mathrm{Treatment} \right) \] 用一个实际的营销案例来说明，假设此刻有两类等量的用户群体^[3]：

User	有广告 CVR	无广告 CVR	Uplift
用户群体 1	\(0.8\%\)	\(0.2\%\)	\(0.6\%\)
用户群体 2	\(2.0\%\)	\(1.7\%\)	\(0.3\%\)

在传统响应模型中，我们可能会向第二类用户投放广告，因为其转化最高。但是在增益模型中，除了广告曝光转化率之外，我们还能知道这两类用户群体在没有广告触达情况下的自然转化率，从而推算出广告所带来的增量。按照这个逻辑，我们更应该向第一类用户投放广告。

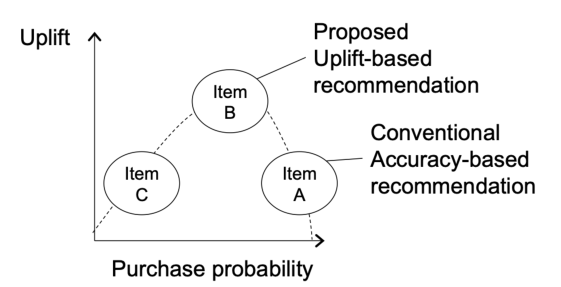
相关概念

因果推断 | Causal Inference

机器学习不过是在拟合数据和概率分布曲线，而变量的内在因果关系并未得到足够的重视。如果要真正解决科学问题，甚至开发真正意义上的智能机器，因果关系是必然要迈过的一道坎。^[1]

• 伪相关性（Spurious Correlation）：深度学习模型能拟合出数据的关联关系，但不能得到因果关系。产生统计关联性有四种情况，而其中两种则是伪相关的。伪相关会造成偏倚（Bias），例如「巧克力销量与诺贝尔奖」的故事，显然二者并没有因果关系。

  

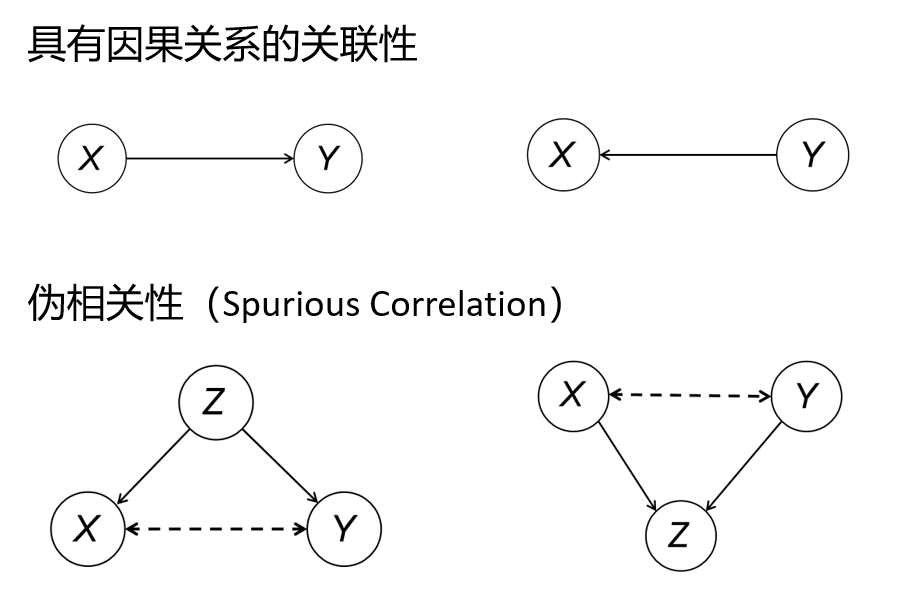
• 混杂（Confounding）：在上述例子中，\(X\) 和 \(Y\) 的共因也被称为混杂因子（Confounder），而当伪相关性和真正的因果关系混合在一起时，就产生了「混杂、有偏」的情形：

  

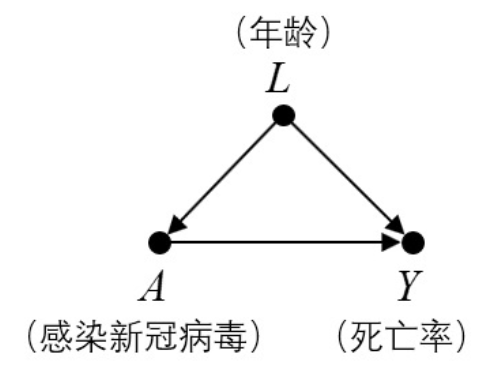
• 消除混杂：一种消除混杂的方法叫后门准则（Backdoor Criterion）。所谓「后门路径」就是第一种伪相关的情况，如果我们有足够的数据能够将所有 \(X\) 和 \(Y\) 之间的后门路径全部阻断（Separation），就可以识别其因果关系。所谓「阻断」，即给混杂因子赋予定值，以这个变量为条件（Conditioning on），缩小到样本的子集后分类讨论。

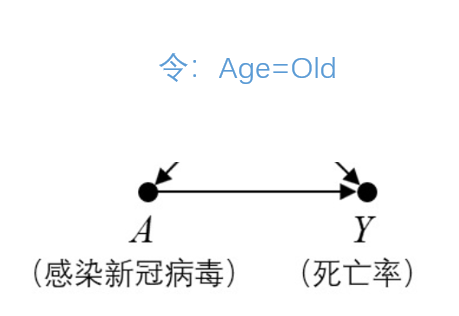
• 干预（Treatment/Intervention）：意为对原始的数据分布加以改变，不同于以变量为条件选取子集，而是直接删除所有指向该变量的边，并直接赋予该变量新的值。在新的模型中检验相关性时，我们就可以发现该变量与目标变量是否真的存在因果关系了。

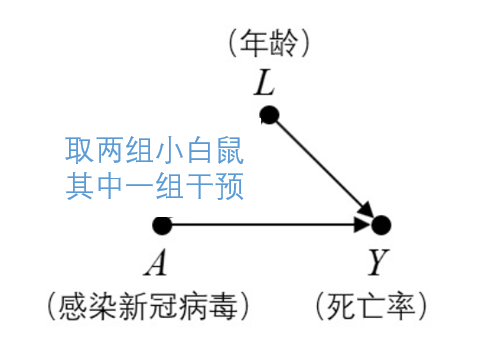
• 反事实推断（Counterfactual inference）：基于数据对外生变量 \(U\)（未观测的变量）进行估算，利用干预改变模型 \(M_x\)（删除所有指向 \(X\) 的箭头），赋予 \(X\) 反事实假设，根据估算的外生变量 \(U\) 和新模型 \(M_x\) 来计算 \(Y\)。

  例如：我们收集到一个事实（用户 A 没收到广告时不会购买），要想知道「收到广告」和「购买」之间是否有因果关系，那我们就需要一个反事实（用户 A 收到广告时会怎么样），但这个数据是不存在的。若想对其进行反事实推理，就要删除所有指向「收到广告」的箭头，包括其他所有特征变量，再对「收到广告」这个变量进行干预。

  此时有一个很重要的「独立假设」：若用 \(Y_1\) 表示收到广告后的购买率，\(Y_0\) 表示没收到广告的购买率，\(T\) 表示我们的干预，则有 \((Y_1,Y_0) \bot T\)，即二者独立。这似乎很难理解，难道不是 \(Y_t\) 不是跟 \(T=t\) 有关吗？然而，不管我们是否推送广告，结果 \(Y_1,Y_0\) 永远是存在的，只是我们需要用 \(T=t\) 来选择「观测」其中的一种，并不会影响其具体的值。

• 整体因果效应（Averaged Treatment Effect, ATE）：一个个体不可能同时使用试验组和对照组的方法分别干预，因此我们只能构建两组非常相似的群组，在相似的群组里进行不同的干预，从而达到反事实推理的目的。在上述「独立假设」下，我们两组的观测结果之差就得到 \(\mathrm{ATE}\)：

\[ \begin{aligned} \tau &=\mathbb{E} \left[ Y_1-Y_0 \right] =\mathbb{E} \left[ Y_1 \right] -\mathbb{E} \left[ Y_0 \right]\\ &=P \left[ Y_1\mid T=1 \right] -P \left[ Y_0\mid T=0 \right]\\ &=P \left[ Y\mid T=1 \right] -P \left[ Y\mid T=0 \right]\\ \end{aligned} \]

• 随机控制试验（Randomized Controlled Trials, RCT）：俗称线上 A/B 测试。为了计算 \(\mathrm{ATE}\)，需要将用户群体进行随机分流，实验组施加干预，测试组保持原先策略。由于完全随机，实验组和对照组的样本在分布上是一致的，因此满足前文提及的「独立假设」，可以直接计算 \(\mathrm{ATE}\)。

• 倾向性评分法（Propensity Score Method，PSM）：在工业界中，做随机实验都会存在一定成本，甚至会引起客户流失，且大多数时候无法完全随机，因此也就没办法去准确估计无偏的 \(\mathrm{ATE}\)。此时实验组和对照组的样本分布存在差异，\(Y\) 和 \(T\) 不再独立使得 \(E\left[ Y_1 \right] \ne E\left[ Y_1\mid T=1 \right]\)，而倾向评分就是用来用来估计「在给定混杂因子的情况下，目标被施加干预」的概率，对概率大的施加一个小的权重，对概率小的施加一个大的权重，用来消除偏倚。

  例如：我们想知道「优惠券的领取」对「购买某商品」的因果效应，于是进行随机控制试验。理想情况下，我们会得到 A 和 B 两组非常相似的群体（性别比例、年龄分布等），其中 A 组「领取优惠券」而 B 组「未领取优惠券」。然而干预因素（发放优惠券）的分配通常不受人为控制：假设女性用户群体可能更热衷于逛淘宝因此领到优惠券的概率更大，则两个组在「性别」这一特征上并不均衡可比，因此无法删除混杂因子指向的边。

  此时我们就需要用到 PSM 来尽可能消除「性别」带来的偏倚。两种常用的倾向性评分方法是近邻匹配（Collaborative Matching, CM）和逆倾向评分加权（Inverse Propensity Score Weighting, IPSW）。^[4]

推荐系统与智能营销

• 点击率（Click Through Rate, CTR）：反映了展品对客户的吸引，具体公式：\(\mathrm{CTR}=点击量/展现量\)。
• 转化率（Conversion Rate, CVR）：用户点击展品到注册、付费的转化率，具体公式：\(\mathrm{CVR}=转化量/点击量\)。
• 投资回报率（Return On Investment, ROI）：具体公式：\(\mathrm{ROI}=总利润/总投资\)。
• 离散干预和连续干预（Treatment）：在营销领域，离散干预可以类比「发不发优惠券」，连续干预可以类比「优惠券的面额」或者「多种优惠券的组合」。现阶段连续干预是推荐系统领域的重大挑战。
• 协同过滤（Collaborative Filtering）：在推荐系统中常用的一种技术，通过收集用户偏好信息，再去寻找相似的商品或者用户群体产生推荐（Item-based 和 User-based）。此外，还有诸如矩阵分解模型、神经网络模型等基于模型的方法。
• 交织列表（Interleaving List）：一种在线评估推荐系统的方法，在信息检索领域最先提出。由于 A/B 测试存在的问题（用于测试的流量不足、重度用户在各组占比不同造成偏倚），使用 Interleaving 则无需分组，只需对所有用户投放一个交织列表，该列表包含两个要比较的模型推荐的结果，通过用户点击哪个多就可以看出哪个模型好。

基本模型

Two-Learner

Two-Learner 是基于双模型的差分响应模型（Differential Response Model），对实验组（有干预）和对照组（无干预）的购买行为进行分别建模，然后用训练所得两个模型分别对待测用户的购买行为进行预测，本质是响应模型^[2]。

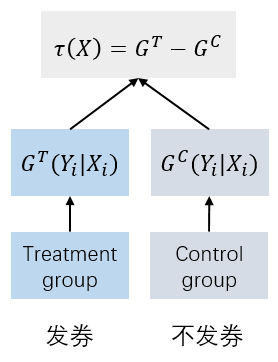
此时一个样本用户可得出两种情况下各自的购买行为预测值。这两个预测值之差就是我们想要的 \(\mathrm{ATE}\)。这种建模方法较简单且易于理解，可以直接用回归、GBDT 等模型实现。然而，Two-Learner 也存在一些局限性：

• 对照组和实验组分别建模，两个模型完全隔离，两个模型容易有累积误差；
• 其次建模的目标是 Response 而不直接是 Uplift，因此模型对 Uplift 的预测能力较有限；
• 干预策略只能是离散值（一种干预对应一个模型），更不能是连续变量。

Single-Learner

Single-Learner 在 Two-Learner 的基础上，将对照组和实验组数据放在一起建模，将实验分组（干预与否）作为一个单独特征，和其他特征一起输入模型中对用户购买行为进行建模。模型的输出是一个条件值，使用其进行预测时，需要计算该样本分别进入实验组和对照组预测两次，将差异作为对 \(\mathrm{ATE}\) 的估计。

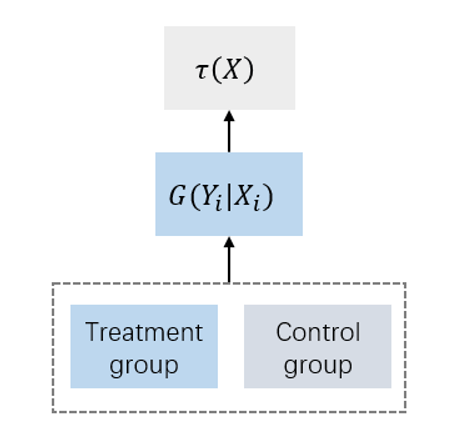
比起 Two-Learner 的优势在于：

• 训练样本共用可以使单个模型学习更加充分，单模型也可以避免双模型打分累积误差较大的问题；
• 模型可以支持干预项为多策略及连续变量的建模，实用性较强。

然而，Single-Learner 在本质上依然还是对 Response 建模，只是分成了两次输出，对 Uplift 的预测还是比较间接^[2]。

标签转换模型

标签转换模型（Class Transformation Method）既可以将实验组与对照组数据打通，同时又是直接对 \(\mathrm{ATE}\) 进行预测，其核心思想是将实验组和控制组样本直接混合并附加新的标签 \(Z\) 满足：

• 当用户在实验组（发券）且用户最终购买时，\(Z=1\)
• 当用户在对照组（无干预）且用户最终未购买时，\(Z=1\)
• 当用户在实验组（发券）且用户最终未购买时，\(Z=0\)
• 当用户在对照组（无干预）且用户最终购买时，\(Z=0\)

可以证明，\(P\left(Z=1\mid T_i\right)\) 和 \(\mathrm{ATE}\) 是线性正相关的，且当实验组与控制组样本比例为 \(1:1\) 时： \[ \tau = 2 P\left(Z=1\mid T_i\right) - 1 \] 假设干预策略 \(T\) 与用户相互独立（满足前文的「独立假设」），则同理 \(T \bot \boldsymbol{X}\)，\(\boldsymbol{X}\) 为所有协变量之和，则有： \[ \begin{aligned} P(Z=1\mid \boldsymbol{X})&=P(Z=1\mid \boldsymbol{X},T=1)P(T=1\mid \boldsymbol{X})+P(Z=1\mid \boldsymbol{X},T=0)P(T=0\mid \boldsymbol{X})\\ &=P(Y=1\mid \boldsymbol{X},T=1)P(T=1\mid \boldsymbol{X})+P(Y=0\mid \boldsymbol{X},T=0)P(T=0\mid \boldsymbol{X})\\ &=P^T(Y_1\mid \boldsymbol{X})P(T=1)+P^C(Y_0\mid \boldsymbol{X})P(T=0)\\ \end{aligned} \] 在 RCT 实验中，当实验组与控制组样本比例为 \(1:1\) 时，\(P(T=0)=P(T=1)=\frac{1}{2}\)，即一个用户被分在两个组的概率是相等的，则有： \[ \begin{aligned} 2P(Z=1\mid \boldsymbol{X})&=P^T(Y_1\mid \boldsymbol{X})+P^C(Y_0\mid \boldsymbol{X})\\ &=P^T(Y_1\mid \boldsymbol{X})+1-P^C(Y_0\mid \boldsymbol{X})\\ \end{aligned} \]

决策树建模

对于 Uplift 直接建模的方式除了上述标签转换的方式外，还有一种就是通过修改已有的学习学习器结构直接对 Uplift 进行建模，比如修改 LR、KNN、SVM 等，比较流行的就是修改决策树模型的特征分裂方法^[3]。

传统决策树模型的分裂过程中，常用的指标是信息增益或信息增益比，其本质是希望通过特征分裂后下游正负样本的分布更加悬殊，即类别纯度变得更高。 \[ \Delta _{\mathrm{gain}}=\mathrm{info}_{\mathrm{after-split}}(D)-\mathrm{info}_{\mathrm{before-split}}(D) \] 同理这种思想也可以引入到 Uplift Model 建模过程，我们希望通过特征分裂后能够把 Uplift 更高和更低的两群人更好地区分开。 \[ \Delta _{\mathrm{gain}}=D_{\mathrm{after-split}}\left( P^T,P^C \right) -D_{\mathrm{before-split}}\left( P^T,P^C \right) \] 其中 \(D\) 的衡量可以基于 KL 散度、欧式距离、卡方距离等。

模型评估

Uplift 十分位柱状图

将测试集预测出的用户按照 Uplift Score 由高到低平均分为 10 组，即依次选取 Top 10%、Top 20% 直到 Top 100% 共十个区间内的用户，分别求每个区间内 Uplift Score 的均值。绘制出如下的十分位柱状图：

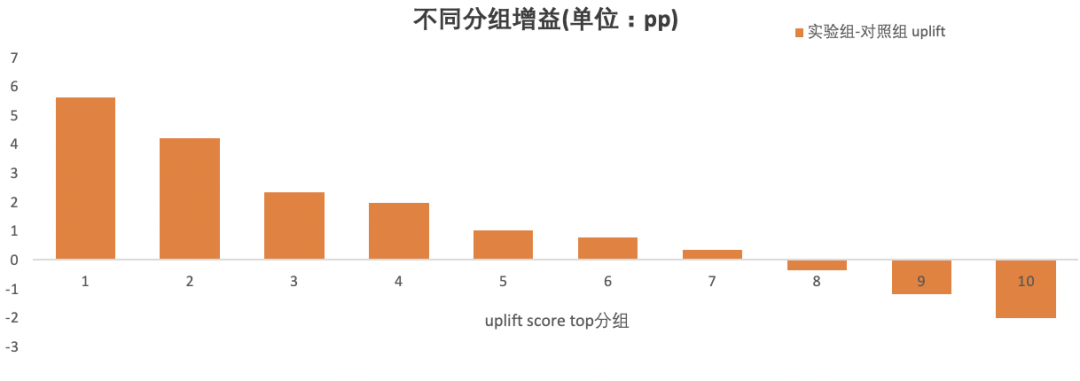
通过观察正负柱子的长短、占比、分布，可以直观地观察到该模型预测的营销增益。如果保留用户区间不变，将每个区间内的 Groud Truth Uplift Score 的均值拿来绘图，则得到的图不一定是有序的柱子。

累计增益曲线 | Qini Curve

计算十分位中累计用户的 Qini 系数，将坐标点连接起来，得到一条累计增益曲线。Qini 系数公式如下： \[ Q(\phi)=\frac{n_{t, y=1}(\phi)}{N_{t}}-\frac{n_{c, y=1}(\phi)}{N_{c}} \] 其中：

• \(\phi\) 是按照 Uplift Score 由高到低排序的用户数量占该组用户数量的比例，\(\phi=0.3\) 代表验组或对照组中 Top 30% 的所有用户；
• \(n_{t, y=1}(\phi)\) 表示在 Top \(\phi\) 用户中，实验组中预测结果为购买的用户数量；同理 \(n_{c, y=1}(\phi)\) 表示对照组预测结果为购买的用户数量；
• \(N_t\) 和 \(N_c\) 则分别代表实验组和对照组总用户样本数。

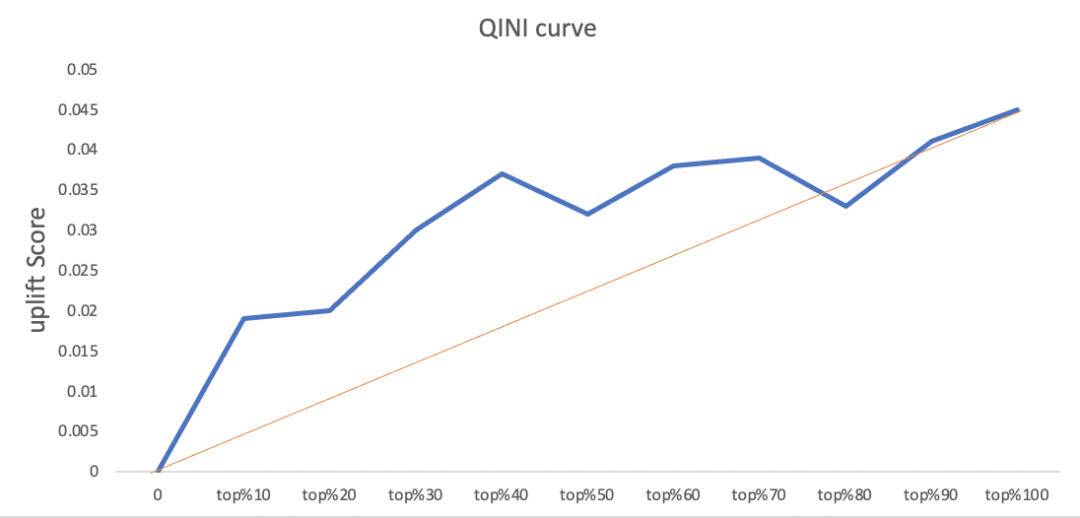
上图中，橙色线是随机曲线（代表随机向人群发放优惠券的增益），Qini 曲线则代表有针对性地向特定人群发放优惠券的增益。

将上图两条曲线作差，可以看到当横轴为 Top 40% 时，Qini 曲线与随机曲线之间距离最大，对应的的纵轴大约是 0.037，这意味着对 Top 40% 用户发放优惠券可以获得最大收益，这部分用户也就是我们需要对其进行营销干预的 Persuadable 人群。相反，如果采用随机发放策略，需要发出 80% 的量才能达到同等效果，大大节约成本。

理论上 Qini 曲线是不应该出现「先下降后上升」的，但是由于模型可能将用户分类到错误区间，因此用 Groud Truth 绘制时可能会有所下降。利用 Groud Truth 的真实区间绘制的图应当是一个光滑的「先上升后下降」曲线，例如下图。

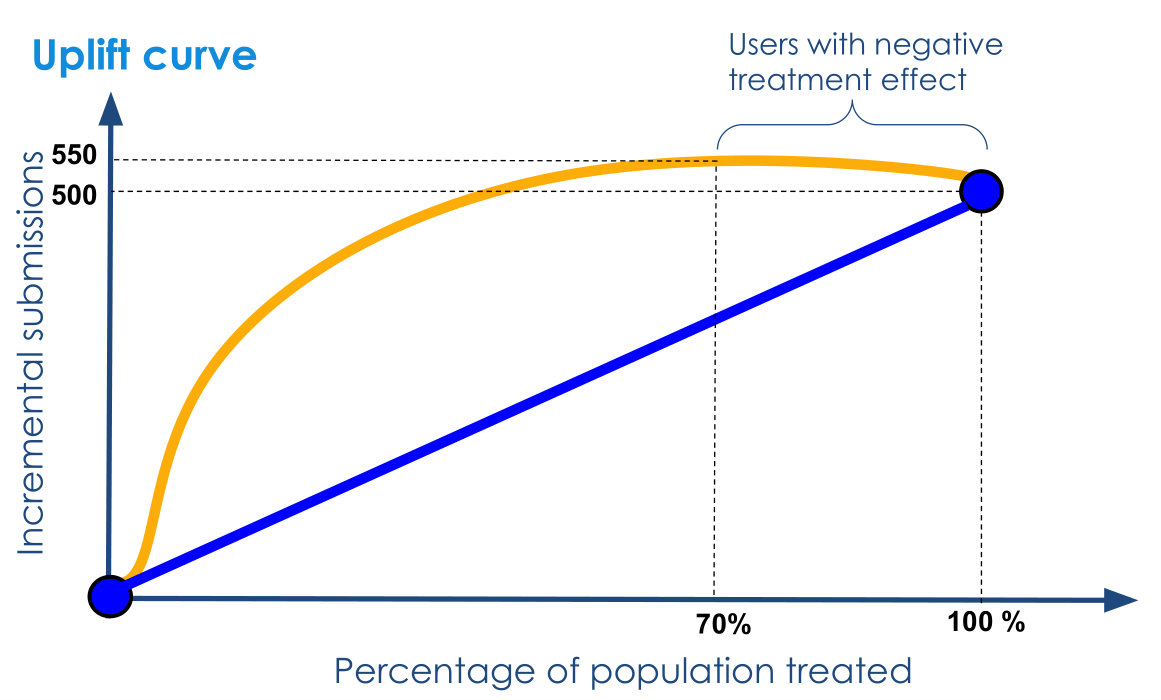
实际应用中，\(\phi\) 的取值越连续，刻画的曲线就越精确平滑，甚至能精确找出 Sleeping Dog 人群。

当实验组和对照组用户数量不平衡，为避免指标失真，会采用另一种累积增益曲线; \[ G(\phi)=\left(\frac{n_{t, y=1}(\phi)}{n_{t}(\phi)}-\frac{n_{c, y=1}(\phi)}{n_{c}(\phi)}\right)\left(n_{t}(\phi)+n_{c}(\phi)\right) \]

AUUC

计算 Qini 曲线和横坐标轴之间的面积，称为 Area Under the Uplift Curve，也称为基尼系数（Qini Coefficient）。该面积越大越好，表示模型结果远超随机选择结果。

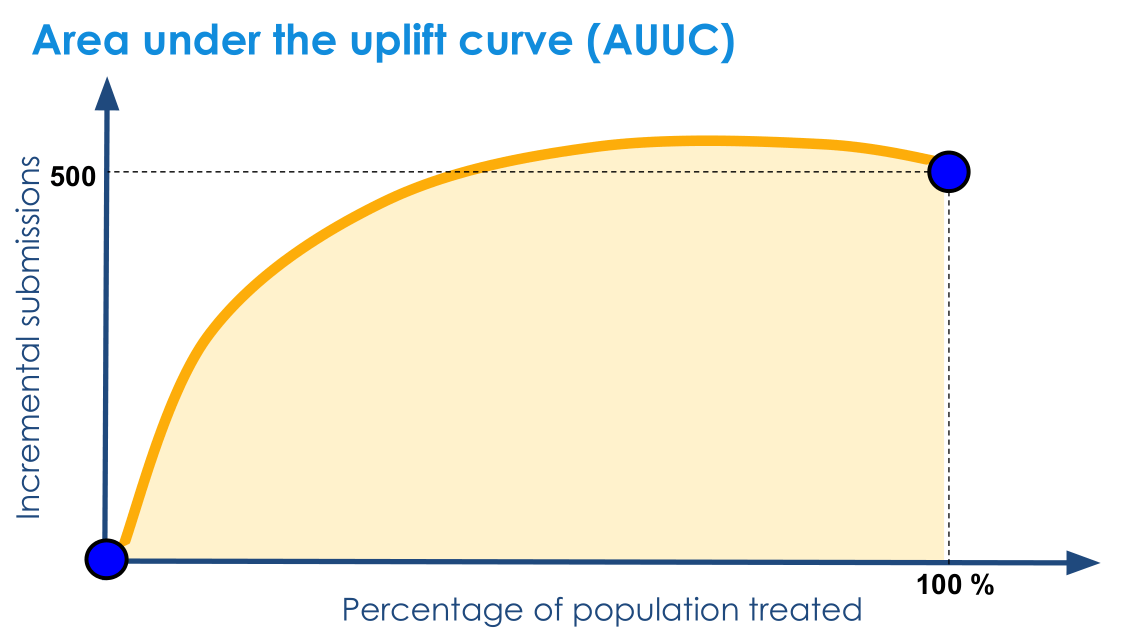
需要注意的是，AUUC 仅用于评价模型，对选取哪些用户发放优惠券并无指导意义。

参考

1. 《因果关系之梯》望止洋 - 知乎专栏 ↩︎
2. 《该把优惠券发送给哪些用户？一文读懂 Uplift 模型》赵小洛 ↩︎
3. 【实践案例分享】阿里文娱智能营销增益模型 ( Uplift Model ) 技术实践，木东居士 - 腾讯云 ↩︎
4. 倾向性评分法（propensity score method，PSM） - 腾讯云 ↩︎