IR学习笔记 #05 检索系统评价

前述文章介绍了几种基本信息检索模型，本文将介绍如何评价一个现有的文档检索系统。

Evaluation in Document Retrieval

一个检索系统的好坏，通常取决于其检索结果与用户查询的相关性，此外还有检索用时、检索范围等等。这里仅针对评价相关性展开讨论。

相关性 | Relevance

如何度量相关性？考虑如下三个待实现的要素：

• A benchmark document collection (基准文档集)

• A benchmark suite of queries (基准查询集)

• A usually binary assessment of either Relevant or Nonrelevant for each query and each document (对基准查询结果打分)

当然，这个「打分标准」可能会随每个人的信息需求而变化（the information need is translated into a query），因此这个指标不是确定的（more than binary）。

有了以上三个基本要素，我们就可以构造出一个合理的测试集：包含文档集、查询集和有关评价机制。

测试集 | Test collections

在制定测试集的时候，往往要先标注好相关的「查询-文档」对。对于小的测试，可以采用人工标注（遍历文档集和查询集）。

但对于较大的测试集则不行（如 TREC 测试集）。此时，可以采用如下方法：

• Pooling | 池化

直接用已有的几个检索系统在「总的基准文档集」中检索，取出每个检索的前 n 个结果，取并集，用这个「新的集合」作为「模拟基准文档集」进行标注，这样就可以大大减少范围。

• Sampling | 抽样

可以通过随机抽样估计真实相关集的大小。

• Search-based

与其阅读所有的文档，不如人工用较宽泛的 Query 先得到一些检索结果，再在这些结果中标记。

有效性度量 | Effectiveness measures

有了合理的测试集，只需要用待测试 IR 查询「基准查询集」的内容，对查询结果与「查询-文档」对比较，即可得到有效性度量。

以下介绍两个在度量有效性过程中常用的变量。

精确率和召回率 | Precision and Recall

在检索结果的 Top n 中，我们定义如下变量：

Precision (精确率): Proportion of a retrieved set that is relevant.

Recall (召回率): Proportion of all relevant documents in the collection included in the retrieved set.

与这两个概念相关的还有 Miss (漏识率) 和 Fallout (误报率)。

对应的混淆矩阵（Confusion Matrix）如下表：

/	相关	不相关
检索到	A	B
未检索到	C	D

\[ \text{精度}=\frac{A}{A+B}, \text{召回率}=\frac{A}{A+C}, \text{漏识率}=\frac{C}{A+C}, \text{误报率}=\frac{B}{B+D} \]

这样的计算过程没有考虑到检索结果的顺序，事实上相关文档排在前列的搜索引擎才是我们最需要的。

有序检索 | Ranked retrieval

考虑搜索引擎返回的结果是有序的，取 Top n，则计算 P/R 的方法可以加以修正：

对检索到的文档按照 ranking 排列，顺次计算 P/R，每次计算时考虑前 k 个文档。最后会得到一组 n 个 P/R 值，再对 Top n 中的「相关文档」对应的 Precision 取平均。

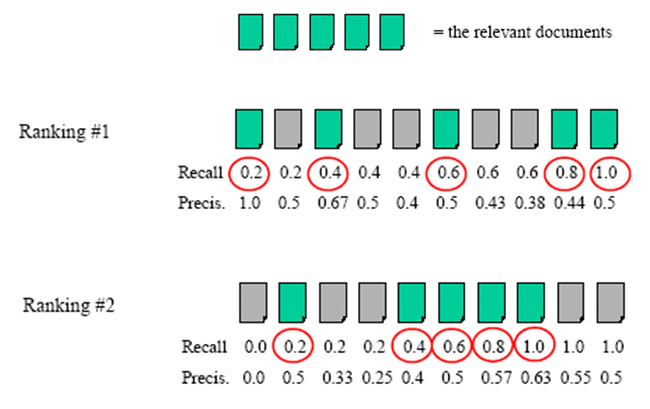
上图中，我们对搜索引擎 A 和搜索引擎 B 查询了同一关键词，并取了 Top 10 的查询结果，其中各有 5 篇相关文档，经过计算可发现，A 的检索结果更优。

但是，如果我们要对同一个搜索引擎 A 用不同的关键词来查询呢？

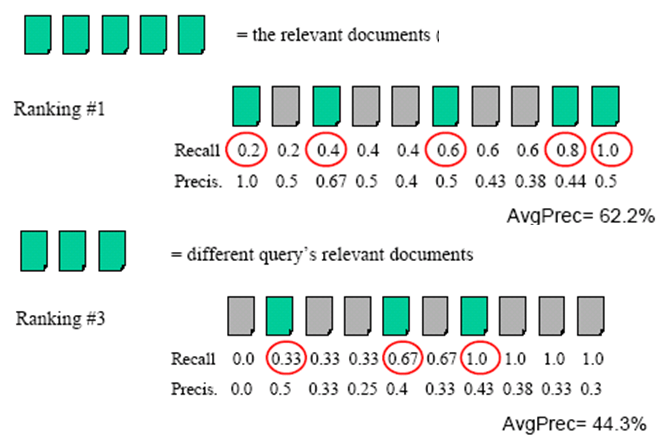
对于不同的 query 可能 Top n 中有数量不同的相关文档，此时的 Recall 就会不一致。如果我们要计算同一 Recall 值处的精度，则需要用到插值方法。

跨查询平均 | Averaging across queries

仅用个别的 query 难以在数据巨大的文档集中得到准确的 P/R 值。因此需要考虑更多的 query，并对结果再次平均。

由此，引出两种平均的思想：

• Micro-average (微平均): each relevant document is a point in the average. 只针对该搜索引擎下一个 query 的命中结果，求出平均精度。
• Macro-average (宏平均): each query is a point in the average (Most Common). 针对该搜索引擎下的许多 query 的微平均精度，再求总的平均精度。

做宏平均的过程中，最重要的是将所有 query 视作平等的点。因为在微平均的过程中，我们往往只关注一些大样本、常见样本，而这些样本并不能完全体现搜索引擎的性能。而宏平均关注其他小样本、偏僻样本，这些样本的检索结果体现了搜索引擎内部的类别分布是否均匀。

这种方法也称作 MAP (Mean Average Precision)，平均之上的平均。

绘图 | Recall/Precision graphs

如果只关注平均精度，则会隐藏检索结果的一些有效信息。如果用图表的形式呈现，则更能观察到趋势。

如果直接把 ranked retrieval 的结果画在图中，会得到一条「锯齿状」的曲线。因为在同一个召回率下，随着结果数的增长，精度是垂直向下的。

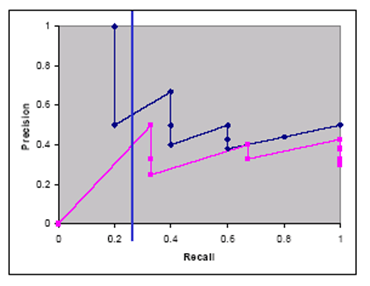
此时，如果我们想要关注曲线中的：

• 特定召回率（10%、20%等）下的精度
• 零召回率（系统尚未返回结果）下的精度

由于各个 query 对应的相关文档总数不同，观测到的召回率点也不同。此时就需要对离散的点用 interpolate (插值)，做出连续的曲线，才能确定这些点的精度。接下来讨论如何选取适合的插值方法。

直接连接各点？连接最大值？连接最小值？连接平均值？

零召回率时假设为零？假设为最大精度？假设为平均精度？与起始点相等？

基本原则：从平均来看，随着召回率的增加，精度应该是单调递减的。

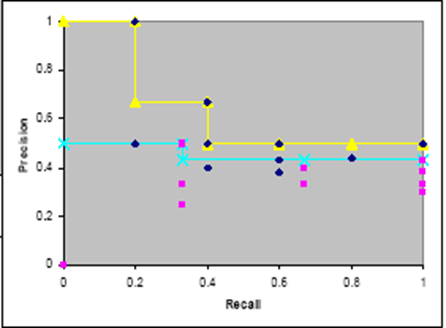
基于这个原则，可以得到 \[ P(R)=\max \left\{P^{\prime}: \quad R^{\prime} \geq R \wedge\left(R^{\prime}, P^{\prime}\right) \in S\right\} \] 即：选取「当前区间」最大的精度点，再以「召回率大于该点的区间」为「新区间」，选取最大的精度点，迭代至 100%。

最后用「阶梯状」曲线连接以上各点，可以得到单调递减的曲线。

E and F

综合考虑 P/R 值，可以计算出如下单值评价指标。

E Measure

用于强调精度或召回率中的某一个指标，同时兼顾另一个指标。

\[ E=1-\frac{1}{\alpha \frac{1}{P}+(1-\alpha) \frac{1}{R}} \] 根据 \(\alpha\) 的取值，增大 \(\alpha\) 代表强调精度的重要性，反之强调召回率。

令 \(\alpha =\frac{1}{\beta ^2+1}\) ，可以得到 \[ E=1-\frac{\left(\beta^{2}+1\right) P R}{\beta^{2} P+R} \] 当 \(\beta = 1\) 时可得到二者相同重要性的效果，此时的 \(E\) 具有的物理意义是所有相关文档 \(A+C\) 和所有检索到文档 \(A+B\) 的集合的对称差的基数除以两个集合的基数。

F Measure

将 \(E\) 取补，可以得到 \[ F_{\beta}=1-E=\frac{\left(\beta^{2}+1\right) P R}{\beta^{2} P+R} \]

其中 \(F_1\) 分数则是 P/R 值的调和平均，较为平均的兼顾了二者。这是分类与信息检索中最常用的指标之一。 \[ F_{1}=\frac{2 P R}{P+R}=\frac{1}{\frac{1}{2}\left(\frac{1}{R}+\frac{1}{P}\right)} \]

之所以使用调和平均而不是算术平均，是因为在算术平均中，任何一方对数值增长的贡献相当，任何一方对数值下降的责任也相当；而调和平均在增长的时候会偏袒较小值，也会惩罚精确率和召回率相差巨大的极端情况，很好地兼顾了精确率和召回率。

单值评价指标 | Other Single-Valued Measures

类似 \(E\) 和 \(F\) 这样的单值评价指标之所以重要，是因为这样能够更好的优化度量。此外，在文档评价中，我们还有如下指标：

• 期望搜索长度 | Expected search length

定义在弱顺序文档，量化的用户查找 K 个相关文档所需工作量。这项指标计算预期用户在找到第 K 个相关文档之前，按顺序浏览搜索结果列表将要看到的非相关文档的数量。

• 损益平衡点 | Breakeven point

寻找 Precision 等于 Recall 的点，通常在分类任务中用到。

• 平均排序倒数 | MRR (Mean Reciprocal Rank)

对于某些 IR 系统（如问答系统或主页发现系统），只关心第一个标准答案返回的 rank，越前越好，这个位置的倒数称为 Reciprocal Rank (RR) ，对问题集合求平均，则得到 MRR。即，把标准答案在被评价系统给出结果中的排序取倒数作为它的准确度，再对所有的问题取平均。