ML学习笔记 #04 逻辑回归:二分类到多分类
本文最后更新于:2022年11月16日 中午
前文介绍了基本的线性回归问题,尝试预测一系列连续值属性。现在我们将介绍的分类问题则关注离散值属性的预测。
在分类问题中,我们尝试预测的结果是否属于某一个类,最基础的就是二元的分类问题(例如预测垃圾邮件、恶性肿瘤),更为复杂的则是预测多元的分类问题。
二分类问题
分类问题的样本与回归问题类似,由特征和目标构成,给定数据集: \[ \left\{\left(x^{(i)},y^{(i)}\right),\;i=1,2,\cdots,m\right\} \] - \(x^{(i)}\) 代表第 \(i\) 个观察实例的 \(n+1\) 维特征向量 \(\left(x_0^{(i)},\cdots,x_n^{(i)}\right)^T\); - \(y^{(i)}\in\{0,1\}\) 代表第 \(i\) 个观察实例的目标变量,在这里有 \(0\) 或 \(1\) 两类结果。
即对于输入的自变量 \(x^{(i)}\),因变量 \(y^{(i)}\) 可能为 \(0\) 或 \(1\)。其中 \(0\) 表示负向类(negative class),\(1\) 表示正向类(positive class)。
我们不对「正向」和「负向」加以特殊区分,但在实际应用中「正向」通常表示「具有我们要寻找的东西」,如垃圾邮件、恶性肿瘤等。
线性回归的不足
首先可能会自然而然地想到用之前的线性回归来解决——用一条直线拟合结果,当预测值大于 \(0.5\) 时归为正向类,反之归为负向类。
这看似合理,然而,线性回归保留了 \(y^{(i)}\) 太多的「信息量」。对于某些「反常样本」,我们可能预测出一个远大于 \(1\) 或者远小于 \(0\) 的结果,同理,这些「反常样本」用于拟合直线时也会对其造成一定偏移,以至于正常样本被归为错误类别。
逻辑回归 | Logistic Regression
线性回归和逻辑回归都属于广义线性模型(Generalized Linear Model)的特殊形式,线性模型都可用于回归问题的求解。但由于逻辑函数(Losistic Function)将结果映射到 Bernoulli 分布,因此逻辑回归更常用于分类问题。
假说表示 | Hypothesis Representation
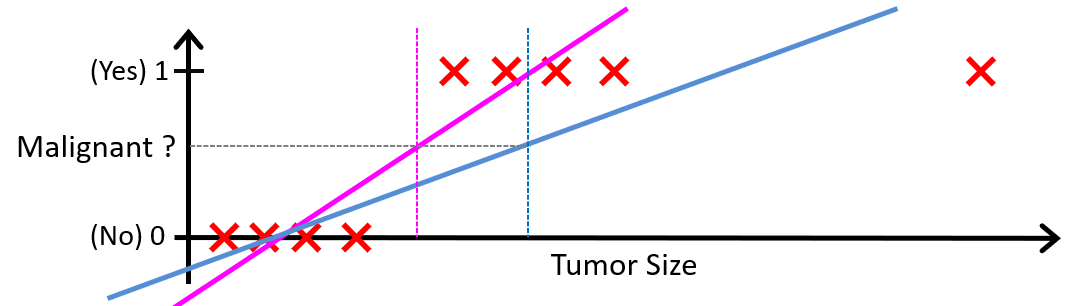
回忆线性回归的假设函数:\(h_\theta(x)=\theta^Tx\),我们在其外套上 \(\text{sigmoid}\) 函数,构造逻辑回归的假设函数为: \[ h_\theta(x)=g\left(\theta^Tx\right)=\frac{1}{1+e^{-\theta^T x}} \]
所谓 \(\text{sigmoid}\) 函数(也即前面提到的逻辑函数): \[ g(z)=\frac{1}{1+e^{-z}} \]
是一个介于 \((0,1)\) 之间的单增 \(S\) 形函数,其导出需要用到 GLMs 和指数分布族(The Exponential Family)的知识。
也就是说,对于一个参数为 \(\theta\) 的逻辑回归模型,输入 \(x\),得到 \(h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}}\) 的预测值。
我们可以把这个输出值视为 \(x\) 这个样本对应的 \(y\) 等于 \(1\) 的概率(estimated probablity),即 \(h_\theta \left( x \right)=P\left( y=1|x;\theta \right)\)。针对分类情形,我们可以认为如果概率 \(\geqslant 0.5\),则分类为 \(1\),否则分类为 \(0\)。
决策边界 | Decision Boundary
又根据 \(\text{sigmoid}\) 函数的性质: \[ h_\theta(x)\geqslant 0.5\iff \theta^Tx\geqslant0 \] 所以只要 \(\theta^Tx\geqslant0\),就会分类为 \(1\),否则分类为 \(0\);于是乎,\(\theta^Tx=0\) 解出的这条「线」(对于高维情形为超平面)被称作决策边界,它将整个空间划分成两块区域(region),各自属于一个分类。
下面看两个二维情形的例子:
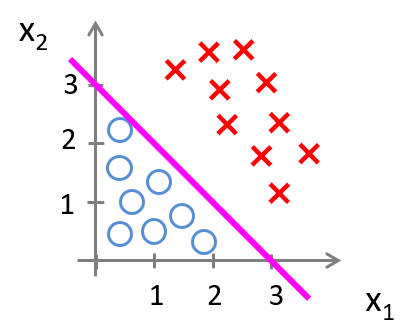
对于上述样本点的分布,用一条直线即可划分空间,对应的假设函数为 \(h_\theta(x)=g\left(\theta_0+\theta_1 x_1+\theta_2 x_2\right)\)。
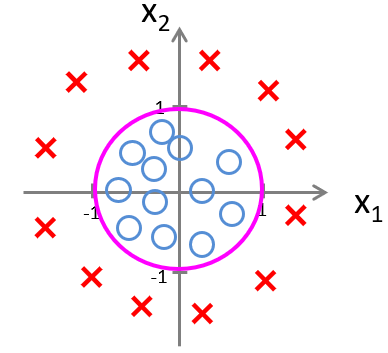
而对于这种分布,我们必须选择二维曲线来划分空间,即使用多项式特征来确定曲线的参数,对应的假设函数为 \(h_\theta(x)=g\left(\theta_0+\theta_1 x_1+\theta_2 x_2+\theta_3 x_3^2+\theta_4 x_4^2\right)\)。当然,我们也可以用更复杂的多项式曲线来划分更复杂的分布。
代价函数
现在,我们的任务就是从训练集中拟合逻辑回归的参数 \(\theta\)。仍然采用代价函数的思想——找到使代价最小的参数即可。
广义上来讲,代价函数是这样的一个函数: \[ J(\theta)=\frac{1}{m}\sum_{i=1}^m\text{Cost}\left(h_\theta(x^{(i)}),y^{(i)}\right) \] 也就是说用每个数据的估计值 \(h_\theta(x^{(i)})\) 和真实值 \(y^{(i)}\) 计算一个代价 \(\text{Cost}\left(h_\theta(x^{(i)}),y^{(i)}\right)\),比如线性回归中这个代价就是二者差值的平方。
理论上来说,我们也可以对逻辑回归模型沿用平方误差的定义,但当我们将 \({h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}x}}}\) 代入到这样的代价函数中时,我们得到的将是一个非凸函数(non-convex function)。这意味着空间中会有许多局部最小值,使得梯度下降法难以寻找到全局最小值。
因此我们重新定义逻辑回归的代价函数: \[ \mathrm{Cost}\left( h_{\theta}(x),y \right) =\begin{cases} -\ln \left( h_{\theta}\left( x \right) \right)& y=1\\ -\ln \left( 1-h_{\theta}\left( x \right) \right)& y=0\\ \end{cases} \] 绘制出的曲线大致呈这样:
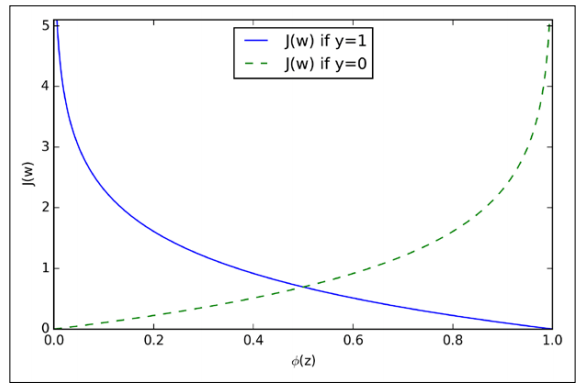
观察曲线,发现当 \(y=1\)(样本的真实值为 \(1\))时,预测值 \(h_\theta(x)\) 越接近 \(1\) 则代价越小,越接近 \(0\) 则代价趋于无穷。譬如在肿瘤分类中,将实际为恶性的肿瘤以百分之百的概率预测为良性,带来的后果将不可估量。
与此同时,注意到代价函数也可以简写为: \[ \mathrm{Cost}\left( h_{\theta}\left( x \right) ,y \right) =-\left[ y\ln \left( h_{\theta}\left( x \right) \right) +\left( 1-y \right) \ln \left( 1-h_{\theta}\left( x \right) \right) \right] \] 它还有另外一个名称——二元交叉熵代价函数(BCE, Binary Cross-Entropy),它又蕴含着怎样的原理呢?
代价函数的数学推导
首先明确什么是一个好的代价函数——当参数 \(\theta\) 使得 \(J(\theta)\) 取极小值时,这个 \(\theta\) 也能使模型拟合效果最好。这时我们回忆起 极大似然估计 的思想:当参数 \(\theta\) 使得 \(L(\theta)\) 取极大值时,这个 \(\theta\) 也能使得事件组最容易发生!
前文已经提到,我们用概率解释预测值 \(h_\theta(x)=P(y=1)\),于是 \(1-h_\theta(x)=P(y=0)\),故: \[ P\left( y=k \right) =\left[ h_{\theta}\left( x \right) \right] ^k\left[ 1-h_{\theta}\left( x \right) \right] ^{1-k},\quad k\in \left\{ 0,1 \right\} \] 而对于数据集 \(\left\{\left(x^{(i)},y^{(i)}\right),\;i=1,2,\cdots,m\right\}\) 下,将其视为已发生的一个事件组,则似然函数为: \[ L\left( \theta \right) =\prod_{i=1}^m{P}\left( y=y^{(i)} \right) =\prod_{i=1}^m{\left[ h_{\theta}\left( x^{(i)} \right) \right] ^{y^{(i)}}}\left[ 1-h_{\theta}\left( x^{(i)} \right) \right] ^{1-y^{(i)}} \] 取对数得到: \[ \ln L(\theta )=\sum_{i=1}^m{\left\{ y^{(i)}\ln \left[ h_{\theta}\left( x^{(i)} \right) \right] +\left( 1-y^{(i)} \right) \ln \left[ 1-h_{\theta}\left( x^{(i)} \right) \right] \right\}} \] 注意到,极大似然法的目标是找到 \(L(\theta)\) 或 \(\ln L(\theta)\) 的极大值,而逻辑回归的目标是找到 \(J(\theta)\) 的极小值,所以自然的,我们将 \(\ln L(\theta)\) 取反来定义 \(J(\theta)\): \[ \begin{aligned} J(\theta)&=-\frac{1}{m}\ln L(\theta) \\ &=-\frac{1}{m}\sum_{i=1}^m{\left[ y^{\left(i\right)}\ln \left( h_{\theta}\left( x^{\left(i\right)} \right) \right) +\left( 1-y^{\left(i\right)} \right) \ln \left( 1-h_{\theta}\left( x^{\left(i\right)} \right) \right) \right]} \end{aligned} \] 其中 \(\frac{1}{m}\) 对要求的 \(\theta\) 没有影响,仅是取一下平均罢了。
可以证明上述代价函数 \(J(\theta)\) 会是一个凸函数,并且没有局部最优值。凸性分析的内容不在本讲的范围,但是可以证明我们所选的代价函数会给我们带来一个凸优化问题(Convex Optimization)。
梯度下降
既然是凸函数,那么现在我们就可以进行梯度下降求解 \(\underset{\theta}{\arg\min }J\left( \theta \right)\) 。
为了求偏导,我们先计算: \[ \begin{aligned} \frac{\partial}{\partial \theta}\mathrm{Cost}\left( h_{\theta}\left( x \right) ,y \right) &=\frac{\partial}{\partial \theta}\left[ -y\ln \left( h_{\theta}\left( x \right) \right) -\left( 1-y \right) \ln \left( 1-h_{\theta}\left( x \right) \right) \right]\\ &=\frac{\partial}{\partial \theta}\left[ y\ln \left( 1+e^{-\theta ^Tx} \right) +(1-y)\ln \left( 1+e^{\theta ^Tx} \right) \right]\\ &=\frac{-yxe^{-\theta ^Tx}}{1+e^{-\theta ^Tx}}+\frac{\left( 1-y \right) xe^{\theta ^Tx}}{1+e^{\theta ^Tx}}\\ &=\frac{-yx+\left( 1-y \right) xe^{\theta ^Tx}}{1+e^{\theta ^Tx}}\\ &=\left( -y+\frac{1}{1+e^{-\theta ^Tx}} \right) x\\ &=\left( h_{\theta}\left( x \right) -y \right) x\\ \end{aligned} \] 于是乎, \[ \frac{\partial J}{\partial \theta}=\frac{1}{m}\sum_{i=1}^m{\left( h_{\theta}\left( x^{\left( i \right)} \right) -y^{\left( i \right)} \right) x^{\left( i \right)}} \] 没错,这个偏导的形式和线性回归完全相同!不同的只是 \({h_\theta}\left( x \right)=g\left( {\theta^T}X \right)\) 的定义——多了一层 \(\text{sigmoid}\) 函数,正是因此,我们不能使用正规方程直接给出解析解,而必须使用梯度下降等方法。
\[ \theta:=\theta-\alpha\cdot\frac{\partial J}{\partial \theta} \]
现在我们对其使用梯度下降即可。另外,在运行梯度下降算法之前,进行特征缩放依旧是非常必要的。
除了梯度下降法,还有很多算法可以用来求解这个最优值:共轭梯度法(Conjugate Gradient)、局部优化法(Broyden fletcher goldfarb shann, BFGS)、有限内存局部优化法(LBFGS)等。
这些算法通常不需要手动选择学习率 \(\alpha\),而是使用一个智能的内循环(线性搜索算法)来选择一个较好的 \(\alpha\),甚至能为每次迭代选择不同的 \(\alpha\)。因此他们有着更优越的常数和时间复杂度,在大型机器学习项目中更加适用。
代码实现
下面以 Coursera 上的二分类数据集 ex2data1.txt 为例,首先看一下数据的分布:
1 | |
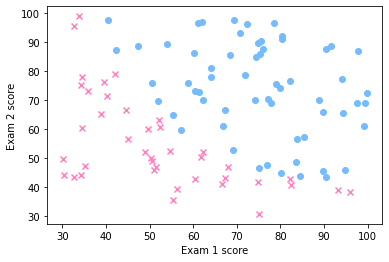
看起来用直线即可划分数据。此外,注意到如果每次都用 np.sum() 计算 \(\sum_{i=1}^m\left(h_\theta(x^{(i)})-y^{(i)}\right)x^{(i)}_j\) 耗时较大,因此将求和化成矩阵形式: \[ \theta :=\theta -\alpha \frac{1}{m}X^T\left( g\left( X\theta \right) -y \right) \] 实现逻辑回归如下,矩阵化后运行时间可缩短一半:
1 | |
得到的 \(\left( \theta_0, \theta_1, \theta_2 \right)\) 结果是:[1.2677 3.0555 2.8289],绘制出决策边界的图像为:
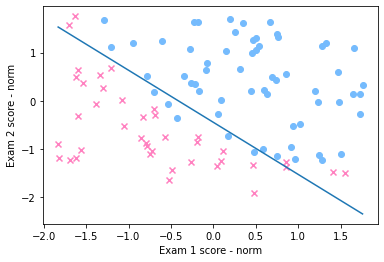
多分类问题
在实际情形中,我们还会使用逻辑回归来解决多元的分类问题。多分类的数据集和二分类相似,区别在于目标变量 \(y^{(i)}\) 在这里不仅有 \(0\) 或 \(1\) 两类结果,还可以取 \(2\)、\(3\) 等更多的数字。
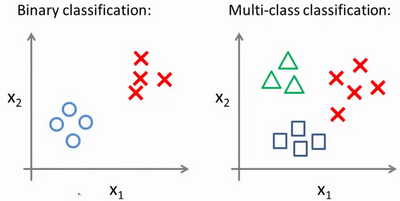
对于接下来要介绍的方法,标签数字的顺序、取法,都不会影响最终的结果。但在某些分类模型中,数值可能具有实际意义,这时候使用独热码(One-Hot)或许是更好的选择。
一对余 | One vs. Rest
对于 \(N\) 分类问题,我们可以将其转化为 \(N\) 个二分类问题——只需创建 \(N\) 个「伪训练集」,每个训练集中仅包含一个类作为正向类,其他 \(N-1\) 个类均视为负向类。
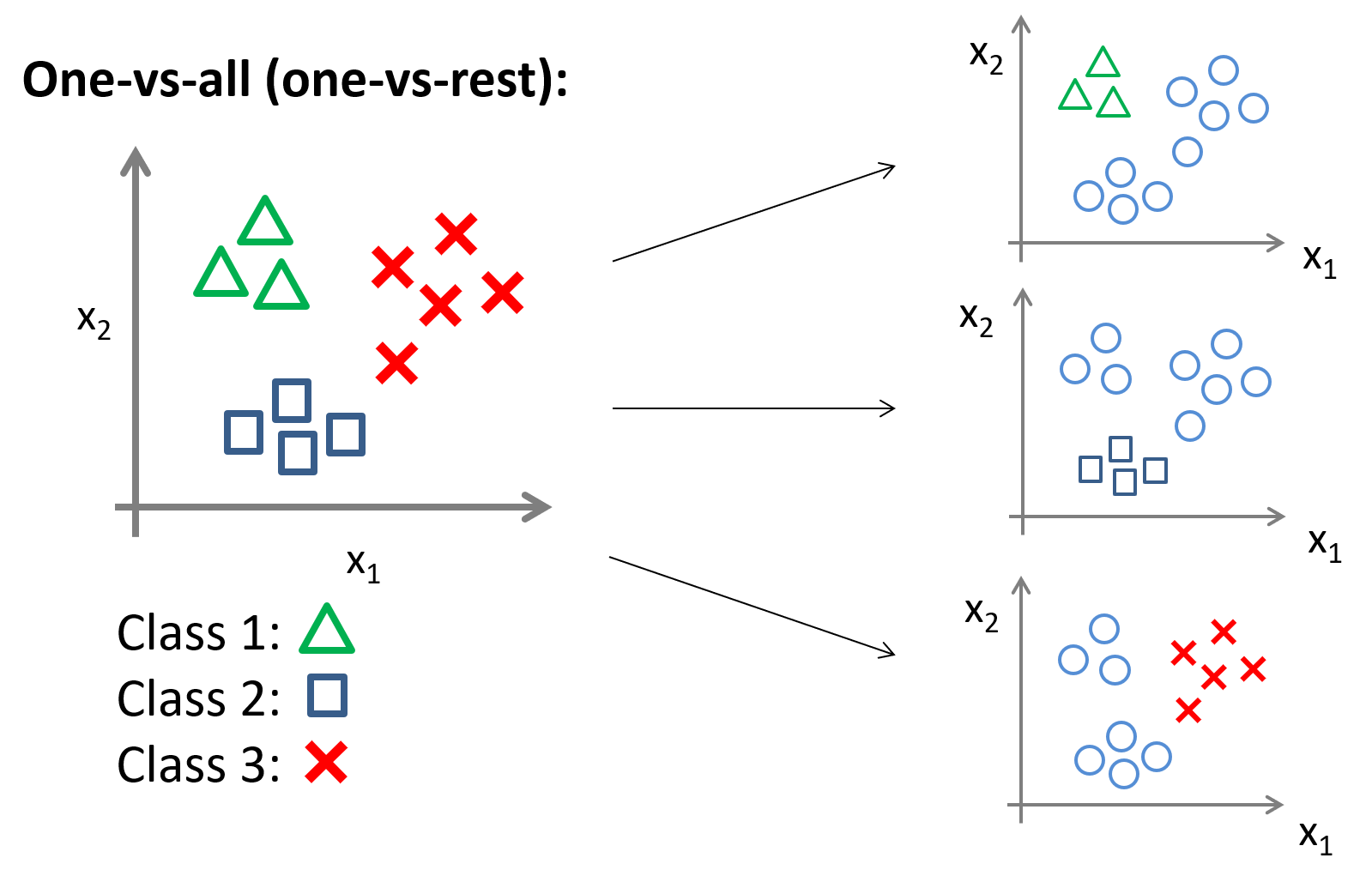
接下来就可以训练 \(N\) 个标准的逻辑回归分类器,将其记为: \[ h_\theta^{\left( i \right)}\left( x \right)=P\left( y=i|x;\theta \right) \;\; i=\left( 1,2,\cdots,N \right) \] 显然,每个分类器的输出都可以视为「属于某类」的概率,在预测时,我们只需要运行一遍所有分类器,然后取其最大值作为预测结果即可。