ML学习笔记 #10 K-Means 聚类

本文最后更新于：2022年12月4日 中午

本文将开始介绍无监督学习。与之前的内容不同，无监督学习的数据不再包含标注的标签，即采用完全无标注的数据集。其中聚类聚类问题属于无监督学习的范畴，其目的是在无标注的情况下将样本集划分为若干类。

本节要介绍的 K-Means 算法就是聚类算法的典型，其中的 \(K\) 指将样本集划分为 \(K\) 个簇（Cluster）。而我们之前介绍过的 KNN 算法，则是一种有监督分类器，其中的 \(K\) 是设定的近邻数量，初学者容易混淆二者。

聚类问题 | Clustering

首先简单介绍一下聚类问题，其本质是「根据样本之间的相似度，将数据进行归类」，由于没有显式的标签，唯一的依据就是样本之间的相似度。而相似度的度量方法，可以大致分为：

  • 距离相似性度量：以欧式距离为代表的各种距离、余弦相似度等。
  • 密度相似性度量：以 KL 散度为代表的各种熵。
  • 连通相似性度量：以杰卡德指数为代表的各种统计量，在集合与图背景下更为常用。

由以上度量方法引申出的聚类算法也有很多：

  1. 基于划分的聚类：K-Means、K-Means++、Bisecting K-Means 等。
  2. 基于密度的聚类：DBSCAN、Mean Shift、OPTICS 等。
  3. 层次聚类：DIANA、AGNES、HDBSCAN、Agglomerative、Divisive 等。
  4. 基于图的聚类：Chinese Whisper、CDP 等。

聚类评价指标

如何评价一个无监督的算法？和有监督类似，仍然需要一个测试集，但无监督算法的测试集则有无标签都可以。针对数据有类别标签的情况，最常用的评价指标有两种：

  • 均一性：每个聚簇中正确分类的样本数占该聚簇总样本数的比例和，类似于精确率，如果一个簇中只包含一个类别的样本，则称其满足均一性。
  • 完整性：每个聚簇中正确分类的样本数占该类型的总样本数比例的和，类似于召回率，同类别样本被归类到相同簇中，则称其满足完整性。

同样，将上述二者加权平均，就能得到类似 \(\mathrm{F} \text {-score}\) 的 \(\mathrm{V} \text {-score}\)。此外，还有：

  • 调节兰德系数（Adjusted Rand index，ARI）：计算聚类结果与实际划分的重叠程度，重叠程度越高表示聚类效果越好。
  • 归一化互信息（Normalized Mutual Information，NMI）：计算聚类结果的簇内互信息，值越大表示聚类结果越相近，效果越好。

对于无类别标签的情况，最常用的指标是轮廓系数（Silhouette Coefficient），结合了内聚度（Compactness）和分离度（Separation）两种因素。简单来说，就是希望簇内样本尽量相近，簇间样本尽量相远，下文将详细介绍。

K-Means 算法

K-Means 算法目的在于寻找最优的 \(K\) 个聚类中心，并将每个样本点归到距离最近的中心点，而聚类中心的优劣显然就取决于能否使距离之和最小化。

如果已知每个样本点的所属类，那很容易就能算出中心（即质心）。如果已知每个类的中心，那么也很容易进行分类（按距离归类）。因此这是一个「先有鸡还是先有蛋」的问题，通过交替迭代计算，直到收敛就能得到两个问题的答案。计算步骤如下：

  1. 首先随机初始化 \(K\) 个聚类中心；
  2. 计算所有点到 \(K\) 个中心的距离，将每个点归到距离最近的中心，得到 \(K\) 类；
  3. 计算 \(K\) 个类的最优聚类中心，即用该类别样本点的平均位置来更新 \(K\) 个中心；
  4. 重复 2-3 步，直到聚类中心不再改变，算法结束。

问题定义

下面将更严谨地给出 K-Means 算法的数学定义，首先我们有数据集： \[ \begin{array}{c} \left\{ x^{(i)}\in \mathbb{R} ^n,i=1,2,\cdots ,m \right\}\\ \left\{ \mu _k\in \mathbb{R} ^n,k=1,2,\cdots ,k \right\}\\ x^{(i)}\rightarrow \mu _{c^{\left( i \right)}}\\ \end{array} \]

  • \(m\) 代表数据集中样本的数量；
  • \(x\) 代表样本特征，是一个 \(n\) 维向量，不需要设定偏置项 \(x_0=1\)；
  • \(K\) 代表设定的目标类别数，为超参数；
  • \(\mu\) 代表聚类中心，共有 \(K\) 个，下标取值为类别编号；
  • \(c^{(i)}\) 代表样本 \(x^{(i)}\) 所属的类别，取值范围也是 \([1,K]\)；
  • \(\mu _{c^{\left( i \right)}}\) 代表样本 \(x^{(i)}\) 所属的聚类中心。

此时我们可以将前文的第 2 步视为： \[ c^{\left( i \right)}:=\underset{k}{\min}\left\| x^{\left( i \right)}-\mu _k \right\| _2^2 \] 这里的距离定义为欧氏距离的平方。第 3 步视为： \[ \mu _k:=\frac{1}{\mathrm{Count}\left( c^{\left( i \right)}=k \right)}\sum_{c^{\left( i \right)}=k}{x^{\left( i \right)}} \] 注意，如果此时对于某个类别 \(k\)，没有数据属于某一聚类中心，即 \(\mathrm{Count}\left( c^{\left( i \right)}=k \right) =0\)，则可以将该聚类中心删去（这样分类数会减少）或者置于随机位置上（保持分类数不变）。

优化目标

经过上文的定义，我们可以引入一个代价函数——残差平方和（Sum of Squared Error，SSE），即各数据点到它所属于的聚类中心的距离之平方和，取均值（Mean）： \[ J\left( c^{(1)},\cdots ,c^{(m)},\mu _1,\cdots ,\mu _K \right) =\frac{1}{m}\sum_{i=1}^m{\left\| x^{\left( i \right)}-\mu _{c^{\left( i \right)}} \right\| _{2}^{2}} \] 很容易证明，2、3 两个步骤都是在减小这个代价：第 2 步减小 \(c^{(i)}\) 引起的代价，第 3 步减小 \(\mu _k\) 引起的代价。所以正确实现的 K-Means 算法的代价应随着迭代次数增加而减小，虽然不是凸函数，但是也可以收敛到局部最优解，不会陷入一直选择质心的循环停不下来。

选取簇数 \(K\)

在实践中，我们可以任取 \(K<m\) 个数据点作为聚类中心。随着聚类簇数 \(K\) 不断增大，样本数据划分会逐渐变得更加精细；因此，随着 \(K\) 不断增大，每个簇的聚合程度会逐渐提高，代价函数 SSE 会逐渐变小。极端情况下，当 \(K=m\) 时，每个样本自成一簇，此时代价函数为 \(0\)。

\(K\) 增大则 \(J\) 减小，绘制出代价函数关于簇数的变化曲线：

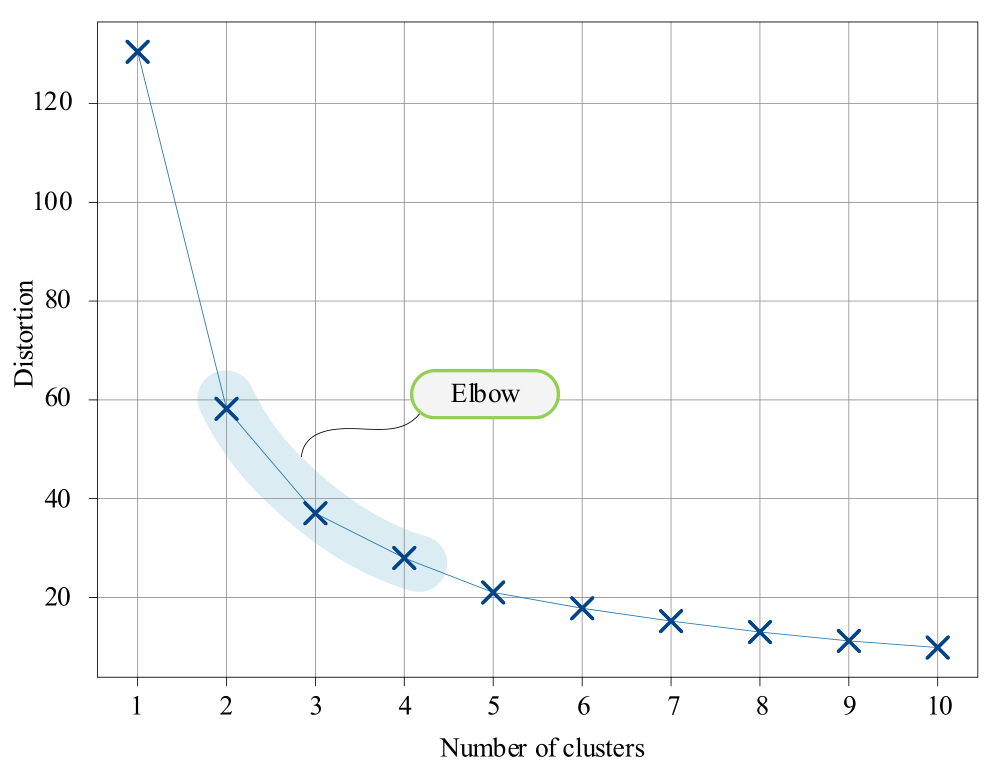
代价函数关于簇数的变化曲线

观察上图，我们发现当 \(K\) 小于「合适的簇数」时，代价函数下降的幅度极大；而当 \(K\) 大于「合适的簇数」时，下降的幅度又逐渐变缓。曲线呈现出「手肘」形状，因此人们通常以手肘法则（Elbow Method）为依据来指导选择这个超参数。手肘法的缺点在于需要人工观察、不够自动化，所以又有了 Gap Statistic 方法，此处不展开介绍。

另一种思路则是从特征空间的角度出发，绘制样本的轮廓图（Silhouette Plot）来选择簇数。轮廓图是针对单个样本 \(x^{(i)}\) 而言的，样本 \(x^{(i)}\) 的轮廓系数（Silhouette Coefficient）可以通过以下方式计算： \[ s^{\left( i \right)}=\frac{b^{\left( i \right)}-a^{\left( i \right)}}{\max \left\{ a^{\left( i \right)},b^{\left( i \right)} \right\}} \] 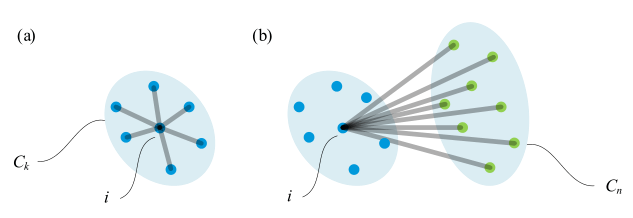第 i 个样本的轮廓图

其中，左图为簇内不相似度 \(a^{\left( i \right)}\)，代表样本 \(x^{(i)}\)，到同簇的其他样本 \(x^{(j)}\) 的距离平均值： \[ a^{\left( i \right)}=\frac{1}{\mathrm{Count}\left( c^{\left( i \right)}=k \right) -1}\sum_{c^{\left( j \right)}=k,i\ne j}{\left\| x^{\left( i \right)}-x^{\left( j \right)} \right\| _{2}^{2}} \] 右图为簇间不相似度 \(b^{\left( i \right)}\)，代表样本 \(x^{(i)}\) 到其他簇样本 \(x^{(j)}\) 的距离平均值的最小值： \[ b^{\left( i \right)}=\underset{k'\ne k}{\min}\frac{1}{\mathrm{Count}\left( c^{\left( j \right)}=k' \right)}\sum_{c^{\left( j \right)}=k'}{\left\| x^{\left( i \right)}-x^{\left( j \right)} \right\| _{2}^{2}} \] 显然，轮廓系数的取值在 \([-1,1]\) 之间，\(s^{\left( i \right)}\) 越趋向于 \(1\)，说明样本 \(x^{(i)}\) 分类越正确；\(s^{\left( i \right)}\) 越趋向于 \(-1\)，说明样本 \(x^{(i)}\) 分类越错误；当 \(s^{\left( i \right)}\) 在 \(0\) 附近时，说明样本 \(x^{(i)}\) 靠近聚类边界。

K-Means 的衍生算法

K-Means 简单易用，方便部署，但是也存在着许多缺点。除了上文提到的簇数 \(K\) 的选择问题，它还有以下缺点：

  • 容易陷入局部最优解；
  • 对噪音、异常点、离群点（Outlier）过于敏感；
  • 单次迭代复杂度高达 \(O(Knm)\)；
  • 对于非凸的数据集难以有效。

针对这些缺点也有许多的衍生算法，下面将简要介绍。

K-Means++

在运行 K-Means 算法时，首先需要随机初始化所有聚类中心点，然而不同的选取方式可能导致不同的收敛结果——停留于局部最优解。例如下图：

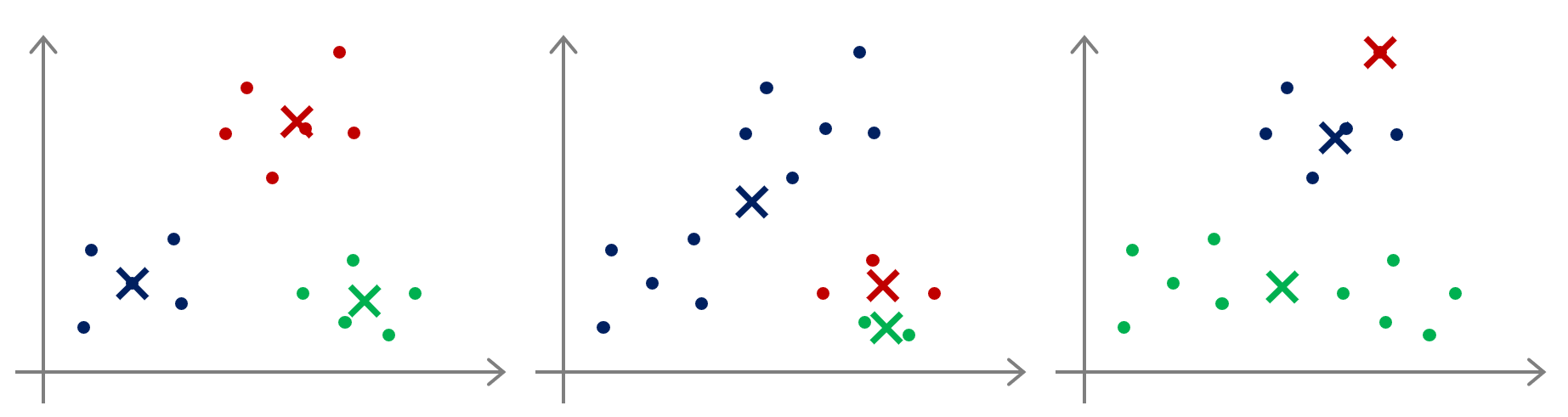
随机初始化导致的局部最优解

比较朴素的做法是多次运行 K-Means 算法，每一次都重新随机初始化，最后选取代价函数最小的结果。这种方法在 \(K\) 较小的时候还是可行的，但是对于 \(K\) 较大的情况需要重复的次数则非常多。

K-Means++ 是最经典的改进算法，其核心思想是：逐个选取聚类中心，且其他距离现有中心越远的样本点越有可能被选为下一个聚类中心。具体步骤如下：

  1. 首先随机选取第一个初始聚类中心 \(\mu_1\)；
  2. 计算每个样本与当前已有聚类中心之间的最短距离，用 \(D(x^{(i)})\) 表示，则该样本被选取为下一个聚类中心的概率为 \(P(x^{(i)})\)；
  3. 重复第 2 步，直到选出 \(K\) 个初始聚类中心。

其中概率 \(P(x^{(i)})\) 的计算方法为： \[ P(x^{\left( i \right)})=\frac{D(x^{\left( i \right)})}{\sum_{j=1}^m{D(x^{\left( j \right)})}} \]

注意，K-Means++ 选点是基于概率，而非直接选择距离最远的点，因为这样很容易陷入离群点，导致一个离群点被单独聚为一类。

Bisecting K-Means

二分 K-Means 算法也是为了改进初始中心选取的问题，它巧妙地规避了「一次选出 \(K\) 个」的问题。其核心思想是：自上而下地逐渐增加簇数，每次选择能最大程度降低代价函数的簇将其划分为两个簇。具体步骤如下：

  1. 首先将所有数据点看作一个簇类；
  2. 对于每一个簇计算簇内的 SSE，同时在每一个簇上单独进行 \(K=2\) 的 K-Means 聚类，计算将该簇一分为二后的总 SSE；
  3. 求出每个簇的两个 SSE 之差，将差值最大者一分为二，并重新更新每个点所属的中心；
  4. 重复第 2-3 步，直到选出 \(K\) 个初始聚类中心。

该方法与层次聚类（Agglomerative Clustering）有点类似但却不同。层次聚类每次选取空间中距离最近的两个点，将其聚为新的「广义点」。最终可以将所有点自下而上聚集为一类，进而自上而下划分为若干类。

K-Mediods

离群点问题带来的影响有很多，直观地就是：如果选中了离群点作为初始聚类中心，大概率会单独聚为一类；即使没有选中，离群点也会给 SSE 带来较大影响，导致预测的聚类中心偏移。

一种可行的方法是通过局部离群因子（Local Outlier Factor，LOF）算法找出离群点，这是一种基于密度的检测方法。此外，还有基于中位数计算的 K-Mediods 聚类。该算法不选用均值，转而采用簇中位置最中心的样本点（Mediods）作为参考点，必须是实际存在的点。选取的准则是所有点到该中心的 SSE。

由于选取的是实际存在的点，那么稀少的离群点肯定不会被选中，也不会导致聚类中心偏移到太远的位置。该方法对于小规模数据是非常有效的，但是注意到选取 Mediods 时需要遍历簇内每一个点，并计算所有距离，所有复杂度是 \(O(n^2)\) 的，比起 K-Means 要慢许多。

Mini Batch K-Means

对于超大规模数据量 \(m\) 的 K-Means，每一轮迭代需要 \(O(Knm)\) 完成，且初值选取不好时需要很多轮次才能收敛，总耗时太久。优化的思路有两个：减少单次迭代的复杂度、减少迭代次数。

其中前者常用的方法有 Elkan K-Means 优化，其在计算样本与聚类中心的距离时，利用三角形关系中的两边之和大于第三边，减少距离计算的次数。该方法可以实现常数级的优化，但依然不够。

后者采用的方法是 Mini Batch（分批处理），通过随机采样得到小规模的数据子集，由于总量很大，采样时能确保数据分布几乎一致。在子集上运行 K-Means 算法能大幅减少收敛时间，并且将聚类中心初始化到一个相对好的位置。具体步骤如下：

  1. 随机采样出部分数据子集，并在子集上使用 K-Means 算法收敛得到 \(K\) 个聚类中心；
  2. 继续采样出部分数据，加到上述的子集中，并将其归到最近的聚类中心；
  3. 更新 \(K\) 个聚类中心；
  4. 重复第 2-3 步，直到所有数据都加入子集。

Kernel K-Means

对于非凸的数据样本，K-Means 往往无法正确聚类：

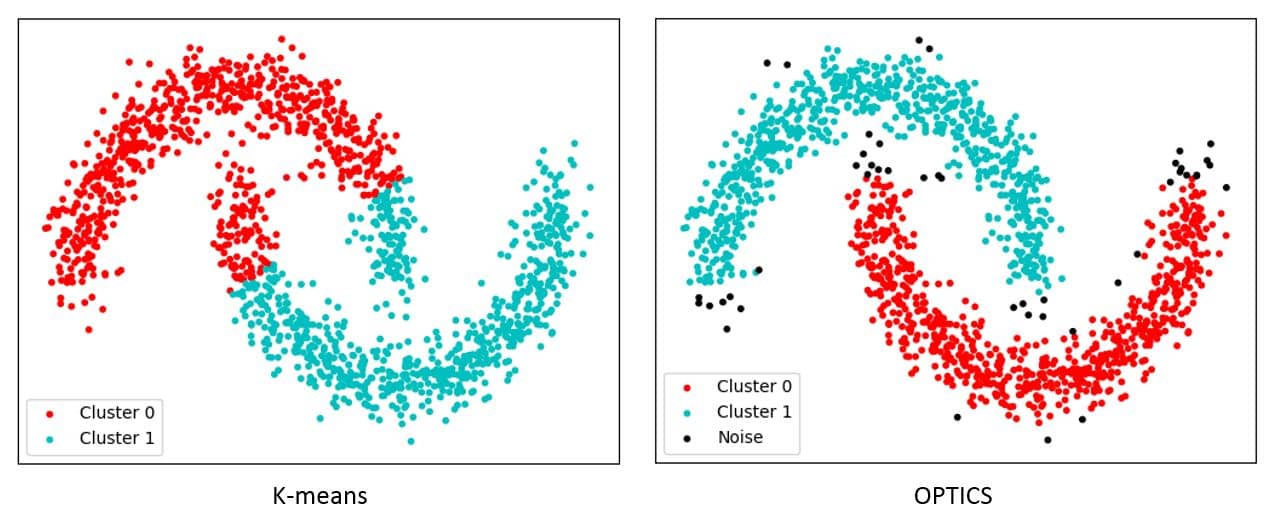
非凸样本的聚类结果

在 ML学习笔记 #9 支持向量机 中我们曾介绍过 Kernel 方法，在 K-Means 中同样也可以使用。此外，基于密度的聚类算法则更加适合于非凸的样本，这里不展开介绍。

练习

平面点集聚类

下面以 Coursera 上的数据集 ex7data2.mat 为例，这是一个三类的平面点集，首先看看数据集的样子：

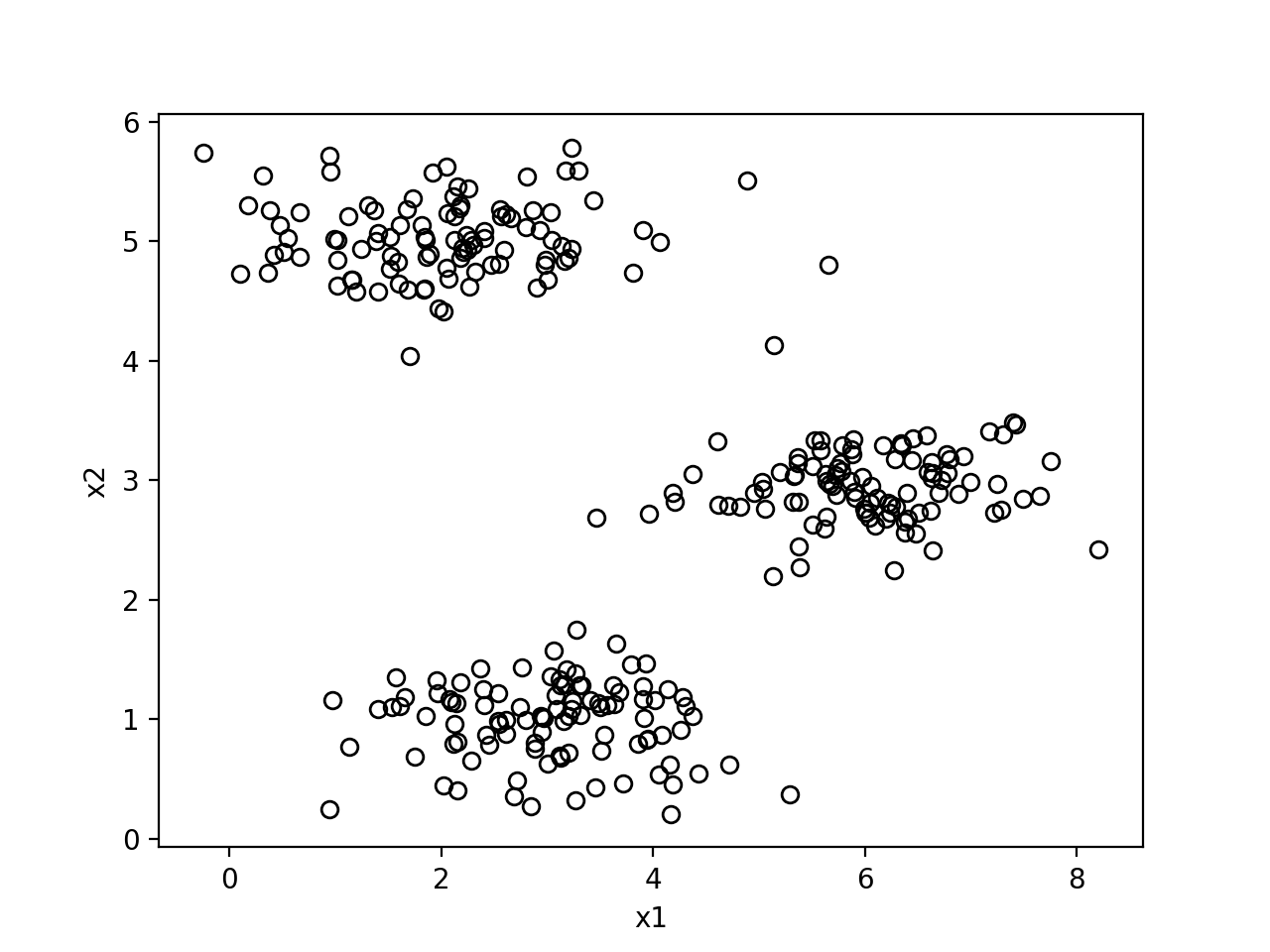
平面点集聚类的原始数据

使用如下代码聚类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

# load data
X = loadmat('ex7data2.mat')['X'] # (300, 2)

# cost function, c := (300,) mu := (K, 2)
def J(X, c, mu):
	m = X.shape[0]
	expand_c = mu[c] # (300, 2)
	return np.linalg.norm(X - expand_c, axis=1, ord=2).sum() / m

# K-Means
def K_means(K, X, times=100):
	(m, n) = X.shape
	best_c, best_mu, best_J = np.empty(m), np.empty((K, n)), np.inf
	for _ in range(times):
		mu = X[np.random.randint(0, m, K)]
		c = np.empty(m, dtype='int')
		while True:
			next_mu = np.zeros((K, n))
			cnt = np.zeros(K)
			for i in range(m):
				c[i] = np.argmin(np.sum(np.square(X[i]-mu), axis=1)) # (X[i]-mu) := (K, 2)
				next_mu[c[i]] += X[i]
				cnt[c[i]] += 1
			next_mu[cnt!=0] /= cnt[cnt!=0][:, np.newaxis]
			next_mu[cnt==0] = X[np.random.randint(0, m, len(cnt[cnt==0]))]
			if (mu == next_mu).all():
				break
			mu = next_mu.copy()
		cost = J(X, c, mu)
		if cost < best_J:
			best_c, best_mu, best_J = c.copy(), mu.copy(), cost.copy()
	return best_c, best_mu

# c.shape = (m,) mu.shape = (K, n)
c, mu = K_means(3, X, times=100)

plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(X[c==0][:, 0], X[c==0][:, 1], 'o', color='blue', markerfacecolor='none', alpha=0.4)
plt.plot(X[c==1][:, 0], X[c==1][:, 1], 'o', color='green', markerfacecolor='none', alpha=0.4)
plt.plot(X[c==2][:, 0], X[c==2][:, 1], 'o', color='red', markerfacecolor='none', alpha=0.4)
plt.plot(mu[0, 0], mu[0, 1], '*', color='blue', ms=10)
plt.plot(mu[1, 0], mu[1, 1], '*', color='green', ms=10)
plt.plot(mu[2, 0], mu[2, 1], '*', color='red', ms=10)
plt.plot([], [], '*', color='black', ms=10, label='cluster centroid')
plt.legend()
plt.plot()

结果如下：

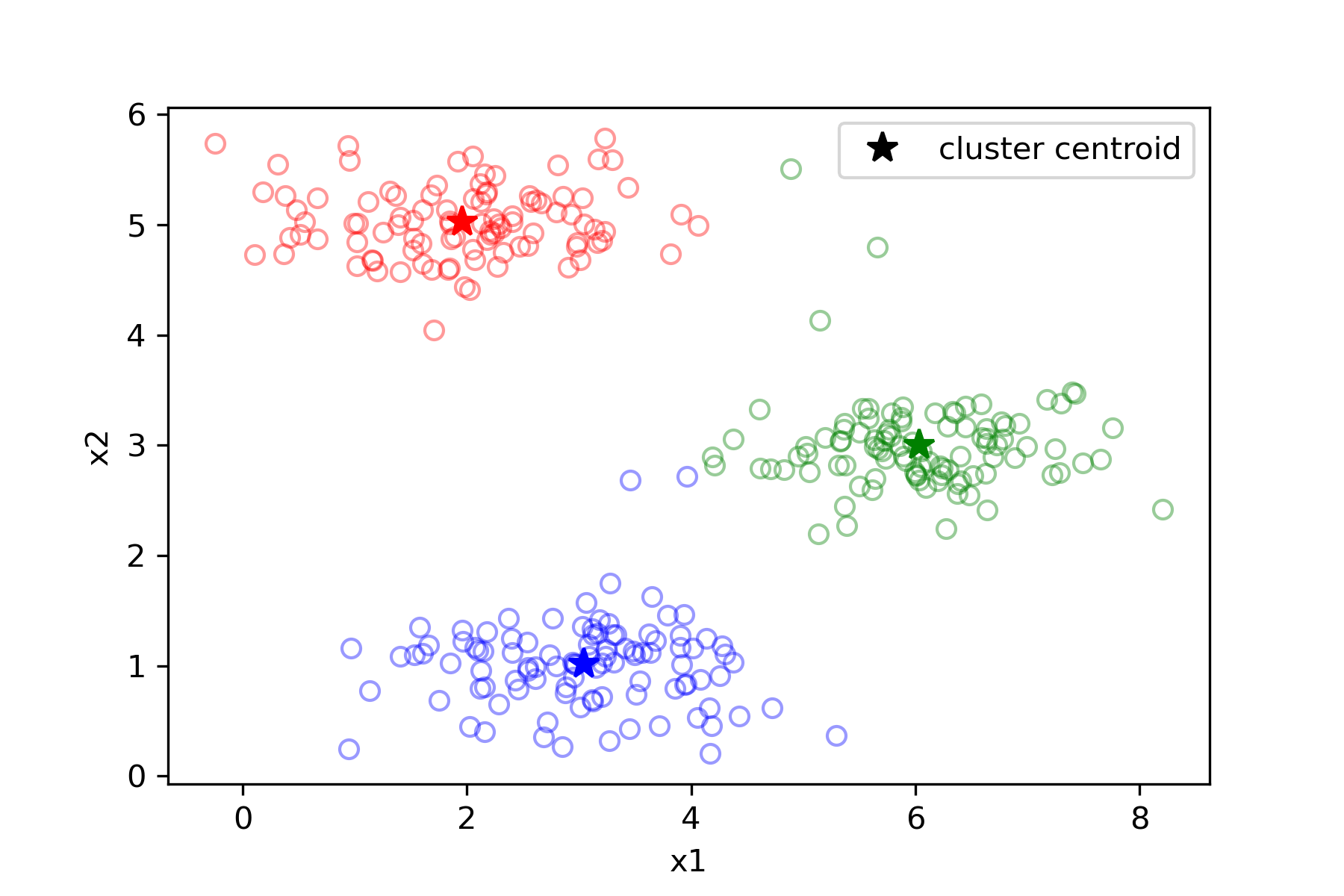
平面点集聚类的结果

图像压缩

图像是有若干像素组成的，每个像素存放 \(3\) 个字节的信息代表其 \(\text{RGB}\) 三通道，三通道可以组成成百上千种颜色，如果可以将其压缩到 \(16\) 种颜色，那么只需要在对应像素位置存放一个 \(4\) 位二进制数即可，这样就把图像压缩到了原来的 \(\frac{1}{6}\) 大小。

现在我们用 K-Means 算法去得到这 \(16\) 种颜色：把原来的所有像素点映射到 \(\text{RGB}\) 空间，再将其聚为 \(16\) 类，得到 \(16\) 个聚类中心用来表示新的压缩像素点。

我们使用的图像含有 \(128\times128\) 个像素，可以处理为 \((128\times128,3)\) 的二维数组，每一行就是一个像素，包含 \(3\) 个值，即 \(\text{RGB}\) 三通道。这就是我们的输入数据。原图如下：

bird_small

使用如下代码聚类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
import numpy as np
from PIL import Image

# load data
def readin():
	data = np.array(Image.open('bird_small.png'))
	data = data.reshape((128*128, 3))
	return data

# cost function
def J(X, c, mu):
	m = X.shape[0]
	expand_c = mu[c] # (300, 2)
	return np.linalg.norm(X - expand_c, axis=1, ord=2).sum() / m

# K-Means
def K_means(K, X, times=100):
	(m, n) = X.shape
	best_c, best_mu, best_J = np.empty(m), np.empty((K, n)), np.inf
	for _ in range(times):
		mu = X[np.random.randint(0, m, K)]
		c = np.empty(m, dtype='int')
		while True:
			next_mu = np.zeros((K, n))
			cnt = np.zeros(K)
			for i in range(m):
				c[i] = np.argmin(np.sum(np.square(X[i]-mu), axis=1))
				next_mu[c[i]] += X[i]
				cnt[c[i]] += 1
			next_mu[cnt!=0] /= cnt[cnt!=0][:, np.newaxis]
			next_mu[cnt==0] = X[np.random.randint(0, m, len(cnt[cnt==0]))]
			if (mu == next_mu).all():
				break
			mu = next_mu.copy()
		cost = J(X, c, mu)
		if cost < best_J:
			best_c, best_mu, best_J = c.copy(), mu.copy(), cost.copy()
	return best_c, best_mu

X = readin()
c, mu = K_means(16, X, times=20)

comImg = np.empty((128*128, 3), dtype='uint8')
for i in range(128*128):
	comImg[i] = np.floor(mu[c[i]])
comImg = comImg.reshape((128, 128, 3))
im = Image.fromarray(comImg)
im.save('bird_compression.png')

压缩后的图片如下：

bird_compression
学习笔记 > 机器学习
#ML
ML学习笔记 #10 K-Means 聚类
https://hwcoder.top/ML-Note-10
作者
Wei He
发布于
2022年2月25日
许可协议