ML学习笔记 #11 主成分分析

本文最后更新于：2022年12月4日中午

我们收集的数据集特征常常包含众多维度，但其中有些维度其实没有存在的必要。最极端的情况就是某一维度是其他若干维度的线性组合，那么这一维度就完全可以丢掉；但现实不会这么精准，如果某一维度是其他若干维度的线性组合加上微小的扰动，其实也可以将其丢掉。

这就是无监督学习中的另一类问题：数据降维（Dimensionality Reduction）。降维的好处有很多，在介绍正规方程时曾提过，冗余特征可能会导致 $X^TX$ 矩阵不可逆。此外，高维特征还可能会造成特征空间稀疏，阻碍模型学习数据，也可能会导致计算量过大的问题。同时，低维特征（$2/3$ 维）也方便进行可视化分析。

数据降维

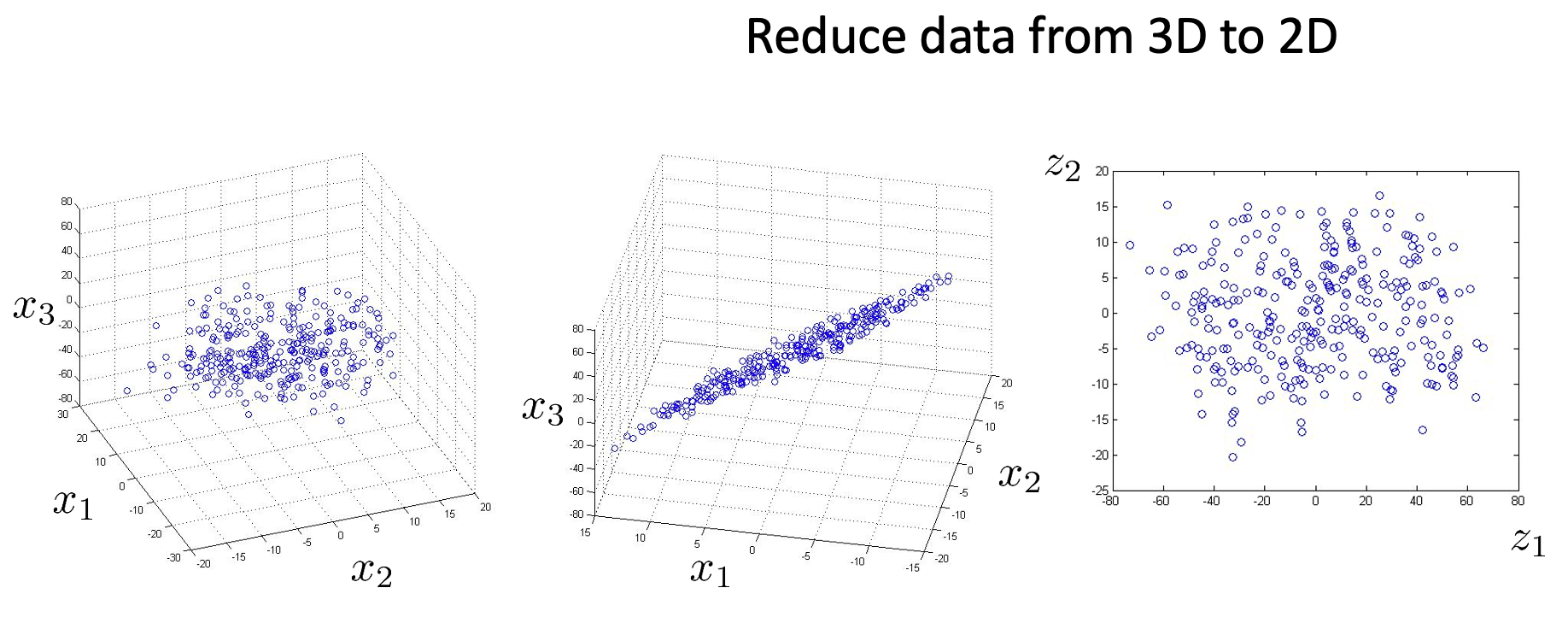
数据降维有众多算法可以完成，主成分分析（Principal Component Analysis，PCA）便是其中之一。

主成分分析 | PCA

主成分分析的基本思想是：假设原始数据的特征有 $n$ 维，我们想将其缩减到 $k$ 维，那么我们只需要在原来的 $n$ 维空间中找到一个 $k$ 维的子空间，使得所有数据到这个子空间的距离平方和最小；此时，原数据在这个子空间上的投影就是我们新的 $k$ 维的数据。

以 $2$ 维数据投影到 $1$ 维为例，我们要做的就是找到一个方向向量，使得将所有数据投影到该向量上时，投影距离平方和最小（最小降维损失理论）。如下图所示，红色直线作为方向向量时，投影距离（垂线段）明显比绿色直线更小，因此我们更倾向于选取红色直线。

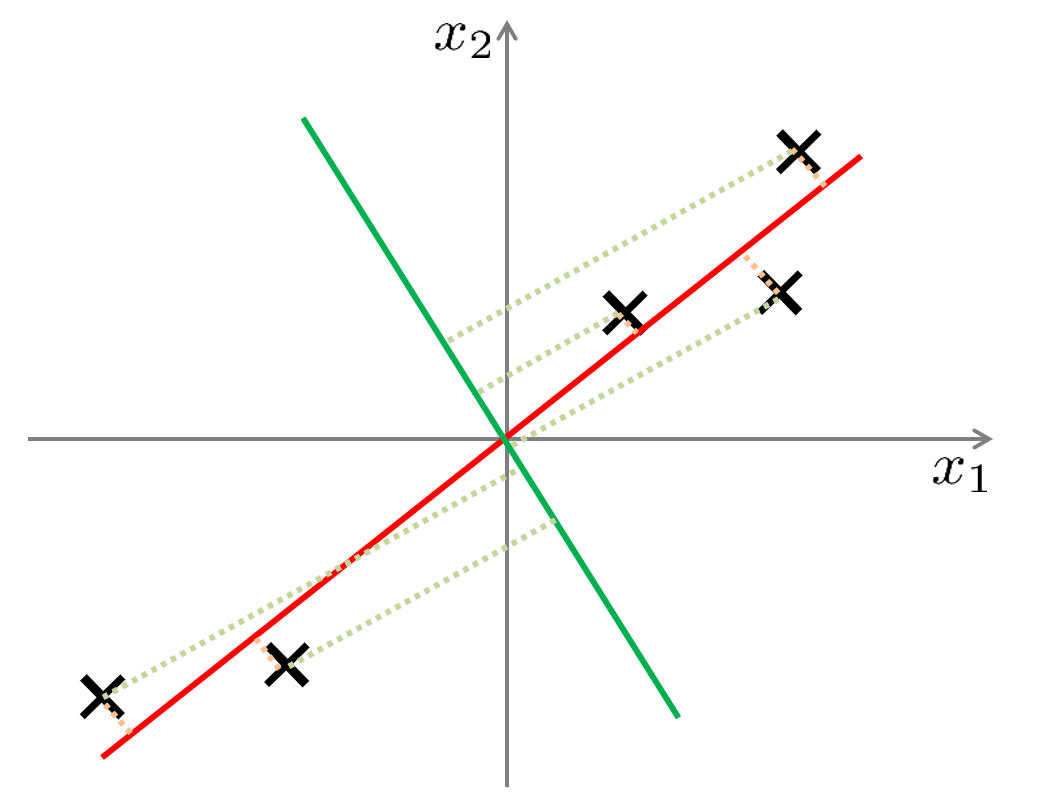
寻找最优的方向向量使得投影误差最小

我们可以直观地理解为：红色直线作为子空间时，极大的保留了原始空间中无标注样本间的特征，原本距离远的点，投影后距离也远（最大方差理论）；而绿色直线则会模糊了原有的特征。下面从数学的角度进行推导。

注意，以上的「寻找方向向量」过程并非线性回归中「寻找拟合直线」，下面一张图可以展现二者的区别：

数学推导

为方便，我们首先将数据均值归一化（Mean Normalization），即使得数据的平均值在原点处。一个获得所需要的 $k$ 维子空间的简单方式是：找到一个合适的 $n$ 维空间，直接选取最重要的前 $k$ 维作为子空间。

具体而言，对于一个数据点 $\mathbf{x}=\begin{bmatrix}x_1\\x_2\\\vdots\\x_n\end{bmatrix}\in\mathbb R^n$，设我们要找的 $n$ 维空间的规范正交基为 $\mathbf{U}^T=[\mathbf{u}_1,\mathbf{u}_2,\cdots ,\mathbf{u}_n]$，则 $x$ 在其中的新坐标为 $\mathbf{y}=\mathbf{Ux}$。其中： \[ y_i=\mathbf{u}_i\cdot \mathbf{x}=u_{i1}x_1+u_{i2}x_2+\cdots +u_{in}x_n \] 它到前 $k$ 维形成的子空间（即以 $\mathbf{u}_1,\mathbf{u}_2,\cdots ,\mathbf{u}_k$ 为基底的子空间）的距离之平方为： \[ {y_{k+1}}^2+{y_{k+2}}^2+\cdots+{y_n}^2 \] 假设我们有 $m$ 个数据 $\mathbf{x}^{(1)},\mathbf{x}^{(2)},\cdots ,\mathbf{x}^{(m)}$，于是我们的优化目标为： \[ \min \sum_{i=1}^m {y^{(i)}_{k+1}}^2+{y^{(i)}_{k+2}}^2+\cdots+{y^{(i)}_{n}}^2 \] 又由于在不同的基下 ${||\mathbf{x}||}^2$ 都是一个定值，于是最小化上述距离等价于最大化下式： \[ \max \sum_{i=1}^m{y_{1}^{\left( i \right)}}^2+{y_{2}^{\left( i \right)}}^2+\cdots +{y_{k}^{\left( i \right)}}^2 \] 其充分条件为： \[ \max \sum_{i=1}^m{y^{(i)}_{r}}^{2},\quad r=1,2,...,k \] 这就是我们的优化目标。由于：

\[ \begin{aligned} \sum_{i=1}^m{y^{(i)}_r}^2&=\sum_{i=1}^m{\left( \mathbf{u}_r\cdot \mathbf{x}^{\left( i \right)} \right) ^2}\\ &=\sum_{i=1}^m{\left( \mathbf{u}_{r}^{T}\mathbf{x}^{\left( i \right)} \right) \left( {\mathbf{x}^{\left( i \right)}}^T\mathbf{u}_r \right)}\\ &=\mathbf{u}_{r}^{T}\left( \sum_{i=1}^m{\mathbf{x}^{\left( i \right)}{\mathbf{x}^{\left( i \right)}}^T} \right) \mathbf{u}_r\\ \end{aligned} \] 是一个正定二次型，$\sum\limits_{i=1}^m {\mathbf{x}^{\left( i \right)}{\mathbf{x}^{\left( i \right)}}^T}$ 是一个正定矩阵，可以进行奇异值分解（SVD，在 IR学习笔记中曾介绍过）： \[ \sum_{i=1}^m{\mathbf{x}^{\left( i \right)}{\mathbf{x}^{\left( i \right)}}^T}=\mathbf{U\Sigma U}^T \] 其中，$\mathbf{U}$ 是正交矩阵，$\mathbf{\Sigma}$ 是对角矩阵 $\begin{bmatrix}\sigma_1&\cdots&0\\\vdots&\ddots&\vdots\\0&\cdots&\sigma_n\end{bmatrix}$，$\sigma_1,\cdots,\sigma_n$ 是奇异值，$\sigma_1>\cdots>\sigma_n$。

奇异值（Singular Value）不同于特征值（Eigen Value），以下摘录自奇异值与特征值辨析：
矩阵作用于特征向量时（$Ax$），只是将 $x$ 乘上一个标量 $\lambda$，相当于将长度缩放了 $\lambda$ 倍。$\lambda$ 可正可负，代表两个方向。
奇异值 $$ 是非负实数，通常从大到小顺序排列。矩阵作用于奇异向量时（$Av$），得到的向量长度就是 $$，最大的 $_1 $ 能使作用后向量最长（对应圆的半径投影到椭圆的长轴），但不能保证方向一致。
特征值一般是对方阵而言的，对于非方阵 $\mathbf{X}$，通常将其乘上自身的转置得到方阵 $\mathbf{X}^T\mathbf{X}$，此时 $\mathbf{X}^T\mathbf{X}$ 的特征值的开方等于 $\mathbf{X}$ 的奇异值。

令 $\mathbf{v}_r=\mathbf{U}^T\mathbf{u}_r$，由于 $\mathbf{U}$ 正交，所以 $\mathbf{v}_r$ 也是单位向量（模为 $1$），代回得到： \[ \begin{aligned} \sum_{i=1}^m{y^{(i)}_r}^2&=\mathbf{u}_{r}^{T}\left ( \mathbf{U\Sigma U}^T \right ) \mathbf{u}_r\\ &=\left( \mathbf{U}^T\mathbf{u}_r \right) ^T\mathbf{\Sigma }\left( \mathbf{U}^T\mathbf{u}_r \right)\\ &=\mathbf{v}_{r}^{T}\mathbf{\Sigma v}_r\\ &=\sigma _1v_{r1}^{2}+\sigma _2v_{r2}^{2}+\cdots +\sigma _nv_{rn}^{2}\\ \end{aligned} \] 所以我们的优化目标变成了： \[ \begin{align} &\max\sum_{i=1}^n\sigma_iv_{ri}^2\\ &\text{s.t.}\begin{cases}\sum\limits_{i=1}^nv_{ri}^2=1\\\sigma_1>\cdots>\sigma_n\end{cases} \end{align} \] 很显然，它的解是：$v_{r1}=1$ 且 $v_{r2}=\cdots=v_{rn}=0$，即 $\mathbf{v}_r=\begin{bmatrix}1\\0\\\vdots\\0\end{bmatrix}$。但是由于 $\mathbf{u}_r$ 正交，所以 $\mathbf{v}_r$ 只能在 $v_{rr}$ 处取 $1$。

又由于 $\mathbf{u}_r=\mathbf{Uv}_r$，所以我们要找的 $n$ 维空间的各个基向量就是矩阵 $\sum\limits_{i=1}^m {\mathbf{x}^{\left( i \right)}{\mathbf{x}^{\left( i \right)}}^T}$ 的各个奇异值对应的奇异向量，我们要降维到的 $k$ 维子空间的各个基向量就是前 $k$ 个奇异向量，对原来的数据进行基变换，就得到了降维后的数据。

算法步骤

总结一下，主成分分析的推导过程稍显复杂，但是它的实现很简单，主要是以下步骤：

计算矩阵 $\sum\limits_{i=1}^m {\mathbf{x}^{\left( i \right)}{\mathbf{x}^{\left( i \right)}}^T}$，更简单的表达是：设矩阵 $\mathbf{X}_{m\times n}=\begin{bmatrix}{\mathbf{x}^{(1)}}^T\\{\mathbf{x}^{(2)}}^T\\\vdots\\{\mathbf{x}^{(m)}}^T\end{bmatrix}$ 为数据集，那么计算样本内积矩阵 $\mathbf{X}^T\mathbf{X}$ 即可；
对 $n\times n$ 的内积矩阵 $\mathbf{X}^T\mathbf{X}$ 进行奇异值分解，得到奇异向量；
选取前 $k$ 个奇异向量作为降维后的空间的基向量，构成基变换矩阵 $\mathbf{C}_{n\times k}$；
对于原数据 $\mathbf{x}$，取 $\mathbf{z}=\mathbf{C}^T\mathbf{x}$ 为其降维后的数据。更简单的表达是：取 $\mathbf{Z}_{m\times k}=\mathbf{X}_{m\times n}\mathbf{C}_{n\times k}$，则 $\mathbf{Z}_{m\times k}$ 是降维后的数据集。

PCA 的算法过程中完全无超参数参与，不需要人为进行干预，最后的结果只与数据有关。这既是优点也是缺点，缺点在于难以利用已有先验进行额外的干预。

主成分数量的选择

那么在实践中，我们到底选择多大的 $k$ 值比较好呢？对此，我们定义一个平均误差为： \[ \frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)}-\mathbf{x}_{\mathrm{approx}}^{\left( i \right)} \right\| ^2} \] 其中，$\mathbf{x}_\mathrm{approx}^{(i)}$ 表示数据 $\mathbf{x}^{(i)}$ 在我们找到的 $k$ 维子空间上的投影。再定义一个总方差为： \[ \frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)} \right\| ^2} \] 则一般的，我们会选择最小的 $k$ 使得： \[ \frac{\frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)}-\mathbf{x}_{\mathrm{approx}}^{\left( i \right)} \right\| ^2}}{\frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)} \right\| ^2}}\leqslant 0.01 \] 并称之为「$99\%$ 的方差得以保留」，这样能使得丢失的信息最小化。

丢失信息越少就越好吗？有时候丢失一部分信息，识别的准确率反而更高了，说明数据集中可能存在噪音特征，而我们将那些噪音丢弃了。但是主成分分析舍弃的特征通常是与标签无关的，在更多时候会不如有监督的 LDA 降维。

此外，上述式子看起来并不好计算，但可以证明，对于给定的 $k$，我们可以借助奇异值（来自 SVD 分解中的 $\mathbf{\Sigma}$ 矩阵）进行计算： \[ \frac{\frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)}-\mathbf{x}_{\mathrm{approx}}^{\left( i \right)} \right\| ^2}}{\frac{1}{m}\sum_{i=1}^m{\left\| \mathbf{x}^{\left( i \right)} \right\| ^2}}=1-\frac{\sum_{i=1}^k{\sigma _k}}{\sum_{i=1}^n{\sigma _i}} \] 由于奇异值衰减非常快，$k$ 不需要很大时上式的值就会低于 $0.01$。

重建压缩数据

作为一种压缩算法，主成分分析也有解压缩的过程，将低维数据还原到高维数据的近似值，也就是前面的 $\mathbf{x}_{\mathrm{approx}}\in\mathbb R^n$。假设我们有压缩后的数据 $\mathbf{z}\in\mathbb R^k$，则只需用基变换矩阵 $\mathbf{C}_{n\times k}$ 倒过来算： \[ \mathbf{x}\approx \mathbf{x}_{\mathrm{approx}}=\mathbf{C}_{n\times k}\mathbf{z} \] 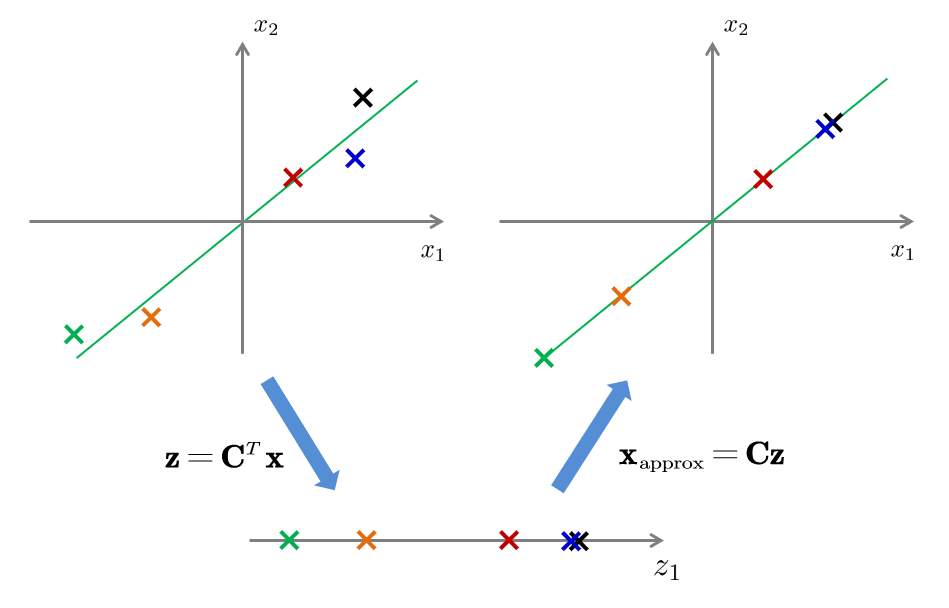重建压缩数据

练习

二维数据压缩到一维

下面以 Coursera 上的数据集 ex7data1.mat 为例，这是一个二维平面上的点集：

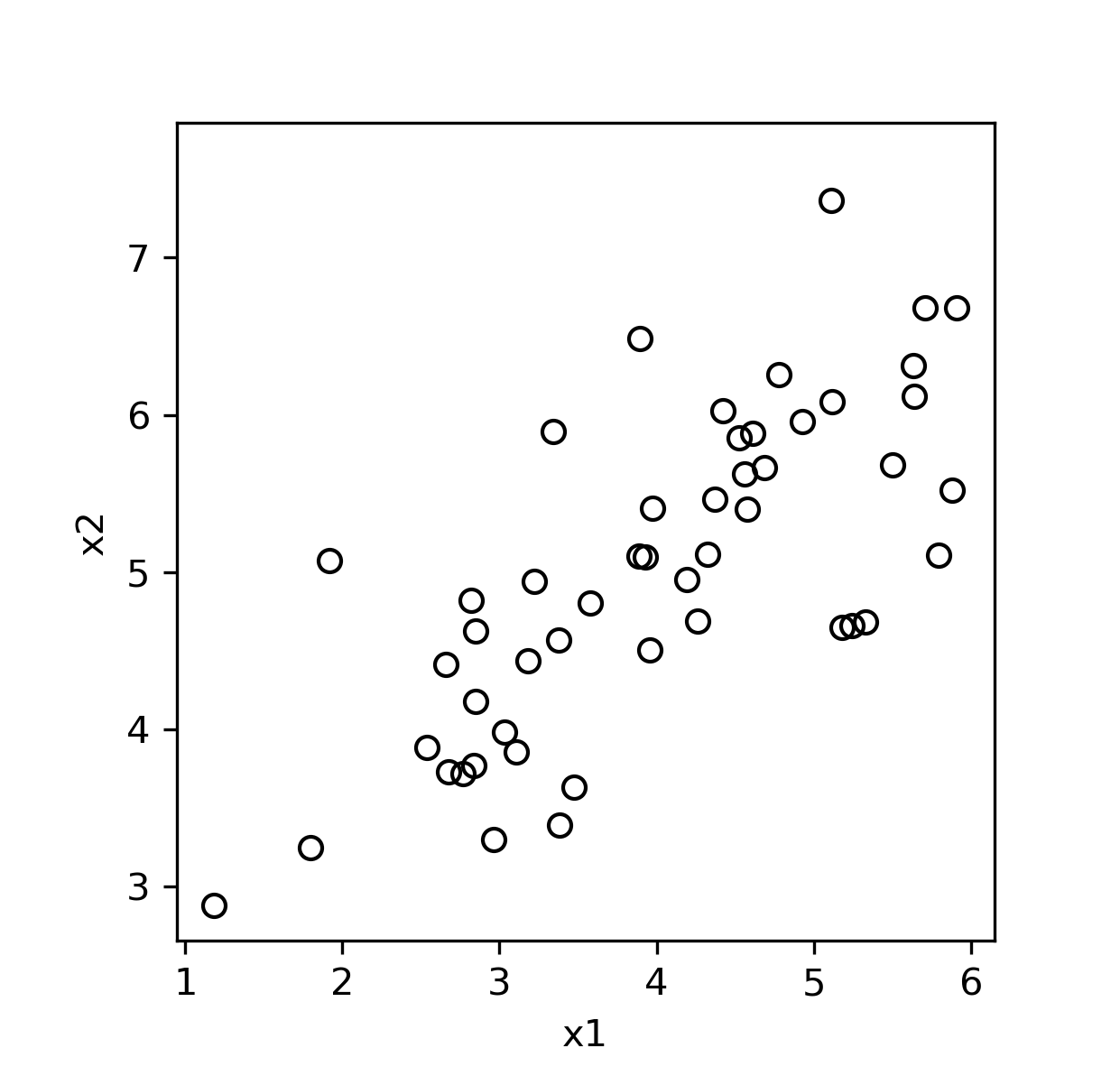
二维平面上的点集

下面我们借助 Numpy 中自带的 np.linalg.svd(arr) 命令实现主成分分析代码：

import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

def PCA(X, dim = -1):
	"""
	X is the input data: (m, n)

	dim is the dimension after reduction
	if dim=-1, then the program select the smallest dim
	such that 99% of variance is retained

	return the data after reduction: (m, dim)
	and the data recovered from reduced data: (m, n)
	"""
	Xmean = np.mean(X, axis=0)
	Xstd = np.std(X, axis=0, ddof=1)
	Xnorm = (X - Xmean) / Xstd   # (m, n)

	U, S, V = np.linalg.svd(Xnorm.T @ Xnorm)
	if dim == -1:
		dim = 1
		while S[:dim].sum() / S.sum() < 0.99:
			dim += 1
	Z = Xnorm @ U[:, :dim]   # (m, dim)
	Xapprox = (Z @ U[:, :dim].T) * Xstd + Xmean  # (m, n)

	return Z, Xapprox

# X.shape = (50, 2)
X = loadmat('ex7data1.mat')['X']
redX, recX = PCA(X, dim=1)

plt.xlabel('x1')
plt.ylabel('x2')
plt.plot(X[:, 0], X[:, 1], 'o', color='black', markerfacecolor='none')
plt.plot(recX[:, 0], recX[:, 1], 'o', color='red', markerfacecolor='none')
plt.axis('square')
plt.show()

得到投影的结果如下：

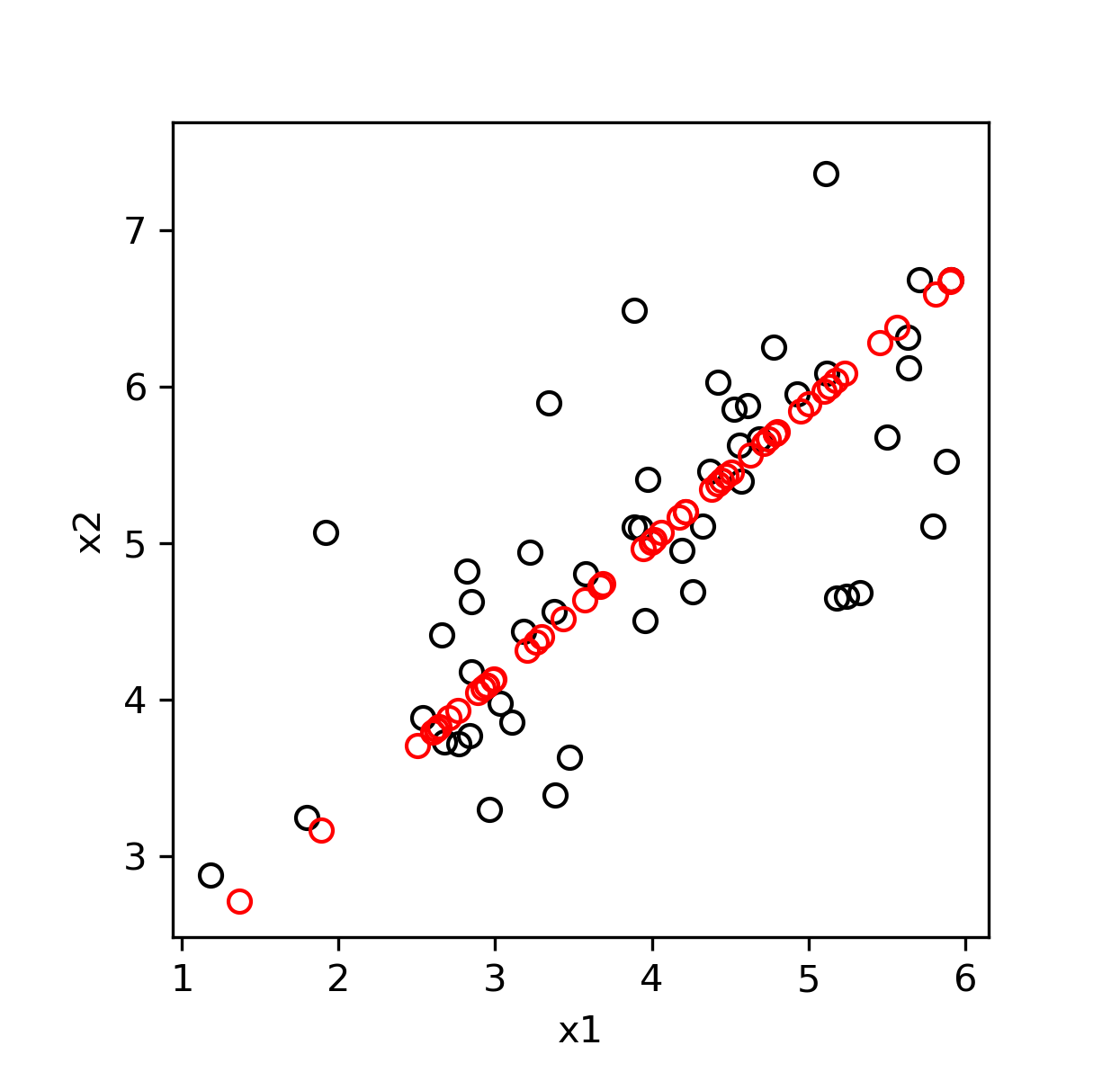
二维数据压缩到一维的结果

人脸特征压缩

数据集 ex7faces.mat 给出了 $5000$ 张人脸照片，每张照片含有 $32\times32$ 的灰度像素，形成维度为 $1024$ 的向量作为其特征。前 $64$ 张照片如图所示：

人脸照片示例

现在将其压缩为 $\text{dim}={36,100}$ 维的数据：

import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt
import matplotlib

X = loadmat('ex7faces.mat')['X'] # (5000, 1024)
X = np.transpose(X.reshape((5000, 32, 32)), [0, 2, 1]).reshape(5000, 1024) # 转置处理
X = -X # 反色

def plot_n_image(X, n):
	""" plot first n images
	n has to be a square number
	"""
	pic_size = int(np.sqrt(X.shape[1]))
	grid_size = int(np.sqrt(n))

	first_n_images = X[:n, :]

	fig, ax_array = plt.subplots(nrows=grid_size, ncols=grid_size,
								sharey=True, sharex=True, figsize=(8, 8))

	for r in range(grid_size):
		for c in range(grid_size):
			ax_array[r, c].matshow(first_n_images[grid_size * r + c].reshape((pic_size, pic_size)), 
						  cmap=matplotlib.cm.binary)
			plt.xticks(np.array([]))
			plt.yticks(np.array([]))

redX, recX = PCA(X, dim=36) # 调用之前写好的 PCA 函数
plot_n_image(recX, n=64)
plt.show()