ML学习笔记 #01 梯度下降:一元线性回归
本文最后更新于:2022年11月23日 上午
该笔记是观看斯坦福大学教授 Andrew-Ng 在 Coursera 上开设的 Machine-Learning 网课所做的笔记。由于网上可见的该课程笔记繁多,而本文所记内容并无不同,仅供个人娱乐。BTW,做笔记的过程中还参考了 xyfJASON 的博客,解答了我许多疑惑。
概论
首先给出两个「机器学习」的定义,尽管对于相关从业者来说,也不存在一个被广泛认可的定义来准确定义机器学习是什么,但或许有助于回答诸如「机器学习是什么?」之类的面试问题:
- Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
- Tom Mitchell (1998) Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
监督学习 | Supervised Learning
如果我们给学习算法一个数据集,这个数据集由「正确答案」组成,然后运用该算法算出更多可能正确的答案,这就是监督学习。
监督学习领域有两大问题:
- 回归(Regression):以一系列离散值(discrete),试着推测出这一系列连续值(continuous)属性。譬如根据已知房价预测未知房价。
- 分类(Classification):以一系列离散值,试着推测出同样是离散值的属性。譬如预测肿瘤的恶性与否。
对于分类问题,输出的结果可以大于两个(分出许多类),输入的特征(feature)也可以更多,例如通过患者年龄和肿瘤大小等特征预测肿瘤的恶性与否。
在绘制这些样本时,可以用一个多维空间中不同颜色的样本点来表示。在一些问题中,我们希望使用无穷多的特征来学习,显然电脑的内存肯定不够用,而后文将介绍的支持向量机(SVM,Support Vector Machine)巧妙地解决了这个问题。
无监督学习 | Unsupervised Learning
对于监督学习里的每条数据,我们已经清楚地知道,训练集对应的正确答案。而在无监督学习中,这些数据「没有任何标签」或是只有「相同的标签」。
因此,我们希望学习算法能够判断出数据具有不同的聚集簇(Cluster),这就是无监督学习领域的经典问题:聚类算(Cluster Algorithm)。
譬如在谷歌新闻中,我们对收集的网络新闻分组,组成有关联的新闻;又如在鸡尾酒宴会问题中,两个位置不同的麦克风录到的两个音源,通过学习算法可以各自分离出来。
一元线性回归 | Univariate Linear Regression
前文提到,回归是监督学习的一个经典问题,这里我们将以线性回归来一窥整个监督学习的模型建立过程。假设已经拥有了回归问题的数据集,我们将之描述为: \[ \left\{\left(x^{(i)}, y^{(i)}\right), i=1,2, \cdots, m\right\} \]
- \(m\) 代表训练集中实例的数量;
- \(x\) 代表特征 or 输入变量;
- \(y\) 代表目标变量 or 输出变量;
- \(({x}^{(i)},{y}^{(i)})\) 代表第 \(i\) 个观察实例;
- \(h\) 代表学习算法的解决方案或函数也称为假设(hypothesis)。
为了解决这样一个问题,我们实际上是要将训练集「喂」给我们的学习算法,进而学习得到一个假设 \(h\)。在本文中,我们尝试用线性函数 \(h_\theta \left( x \right)=\theta_{0} + \theta_{1}x\) 拟合之。因为只含有一个特征 or 输入变量,因此这样的问题叫作一元线性回归问题。
代价函数 | Cost Function
有了上文建立的基础模型,现在要做的便是为之选择合适的参数(parameters)\(\theta_{0}\) 和 \(\theta_{1}\),即直线的斜率和在 \(y\) 轴上的截距。
选择的参数决定了得到的直线相对于训练集的准确程度,模型所预测的值与训练集中实际值之间的差距就是建模误差(modeling error)。我们要做的就是尽量选择参数使得误差降低,即最小化 \(h_{\theta}(x^{(i)})\) 和 \(y^{(i)}\) 的距离。于是我们有了经典的平方误差代价函数: \[ J\left( \theta _0,\theta _1 \right) =\frac{1}{2m}\sum_{i=1}^m{\left( h_{\theta}(x^{(i)})-y^{(i)} \right) ^2} \] 也即是每个数据纵坐标的预测值与真实值的差的平方之和的平均,除以 2 仅是为了后续求导方便,没有什么本质的影响。
绘制一个三维空间,三个坐标分别为 \(\theta_{0}\) 和 \(\theta_{1}\) 和 \(J(\theta_{0}, \theta_{1})\),对每个 \(\left( \theta_0, \theta_1 \right)\) 对,代入训练集可以得到一个 \(J(\theta_{0}, \theta_{1})\) 值,经过一系列计算,我们得到一个碗状曲面:
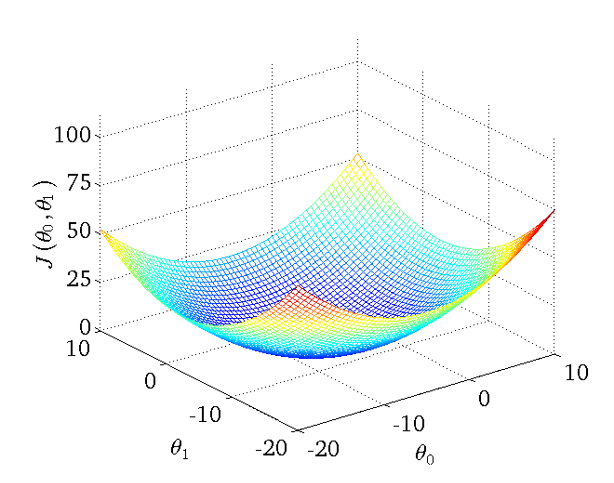
显然,在三维空间中存在一个使得 \(J(\theta_{0}, \theta_{1})\) 最小的点。为了更好地表达,我们将三维空间投影到二维,得到等高线图(Contour plot):
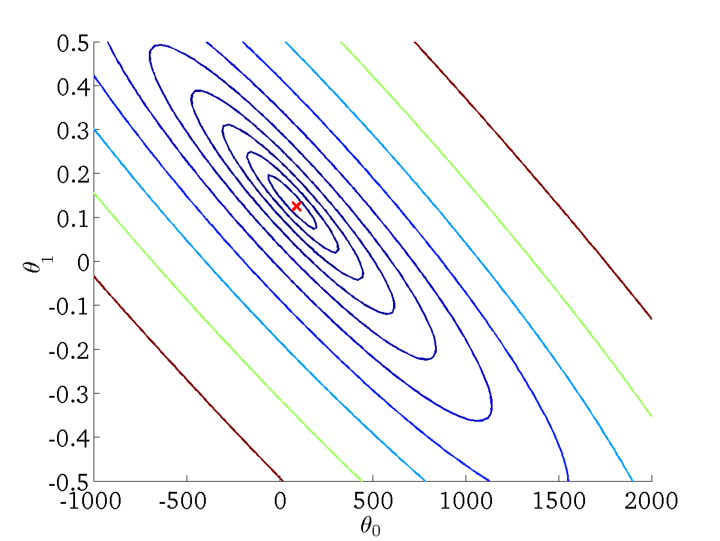
这些同心椭圆的中心,就是我们要找到使得 \(J(\theta_{0}, \theta_{1})\) 最小的点。
梯度下降法 | Gradient Descent
在数学上,我们知道最小二乘法可以解决一元线性回归问题。现在有了等高线图,我们需要的是一种有效的算法,能够自动地找出这些使代价函数 \(J\) 取最小值的 \(\left( \theta_0, \theta_1 \right)\) 对。当然并不是把这些点画出来,然后人工读出中心点的数值——对于更复杂、更高维度、更多参数的情况,我们很难将其可视化。
梯度下降是一个用来求一般函数最小值的算法,其背后的思想是:开始时随机选择一个参数组合\(\left( \theta_{0},\theta_{1},......,\theta_{n} \right)\),计算代价函数,然后一点点地修改参数,直到找到下一个能让代价函数值下降最多的参数组合。
持续这么做会让我们找到一个局部最小值(local minimum),但我们无法确定其是否就是全局最小值(global minimum),哪怕只是稍微修改初始参数,也可能最终结果完全不同。当然,在一元线性回归问题中,生成的曲面始终是凸函数(convex function),因此我们可以不考虑这个问题。
在高等数学中,我们知道「下降最多」其实指的是函数 \(J\) 的梯度方向的逆方向,也即方向导数最大的方向,梯度定义为: \[ \nabla J=\mathrm{grad} J=\left\{ \frac{\partial J}{\partial \theta _0},\frac{\partial J}{\partial \theta _1} \right\} \] 所以不断迭代进行赋值: \[ \theta_j:=\theta_j-\alpha\cdot\frac{\partial}{\partial\theta_j} J(\theta_{0}, \theta_{1}) \] 直到收敛,即可找到一个极小值。其中,\(\alpha\) 就是这一步的步长,也称为学习率(Learnig rate)。学习率的选取很重要,过小则梯度下降很慢,过大则有可能不收敛。
数学推导
对代价函数求偏导:
\(j=0\) 时:\(\frac{\partial}{\partial \theta _0}J(\theta _0,\theta _1)=\frac{1}{m}\sum_{i=1}^m{\left( \theta _1x^{(i)}+\theta _0-y^{(i)} \right)}\)
\(j=1\) 时:\(\frac{\partial}{\partial \theta _1}J(\theta _0,\theta _1)=\frac{1}{m}\sum_{i=1}^m{x^{(i)}\left( \theta _1x^{(i)}+\theta _0-y^{(i)} \right)}\)
所以梯度方向为: \[ \mathrm{grad } J=\left\{ \frac{\partial J}{\partial \theta _0},\frac{\partial J}{\partial \theta _1} \right\} =\left\{ \frac{1}{m}\sum_{i=1}^m{\left( \theta _1x^{(i)}+\theta _0-y^{(i)} \right)},\frac{1}{m}\sum_{i=1}^mx^{(i)}\left( \theta _1x^{(i)}+\theta _0-y^{(i)} \right) \right\} \]
此外,我们注意到在每一步迭代过程中,我们都用到了所有的训练样本,如 \(\sum_{i=1}^mx^{(i)}\)、\(\sum_{i=1}^my^{(i)}\)、\(\sum_{i=1}^mx^{(i)}y^{(i)}\) 等项,这也称为批量梯度下降(Batch Gradient Descent)。
代码实现
需要注意的是,迭代赋值的过程中,\(\left( \theta_0, \theta_1 \right)\) 的值要同时更新,否则就会与梯度方向有微小区别。用 Python 元组解包赋值可以实现,用矩阵乘法也可实现。
为了用向量化加速计算,这里利用了一个小性质,就是当 \(a\) 和 \(b\) 都为向量时有 \(a^Tb=b^Ta\),所以有: \[ X\theta =\left[ \begin{array}{c} -\left( x^{(1)} \right) ^T\theta -\\ -\left( x^{(2)} \right) ^T\theta -\\ \vdots\\ -\left( x^{(m)} \right) ^T\theta -\\ \end{array} \right] =\left[ \begin{array}{c} -\theta ^T\left( x^{(1)} \right) -\\ -\theta ^T\left( x^{(2)} \right) -\\ \vdots\\ -\theta ^T\left( x^{(m)} \right) -\\ \end{array} \right] \] 下面以 Coursera 上的一元线性回归数据集 ex1data1.txt 为例实现代码:
1 | |
得到的 \(\left( \theta_0, \theta_1 \right)\) 结果是:[-3.8953 1.1929],作图如下:
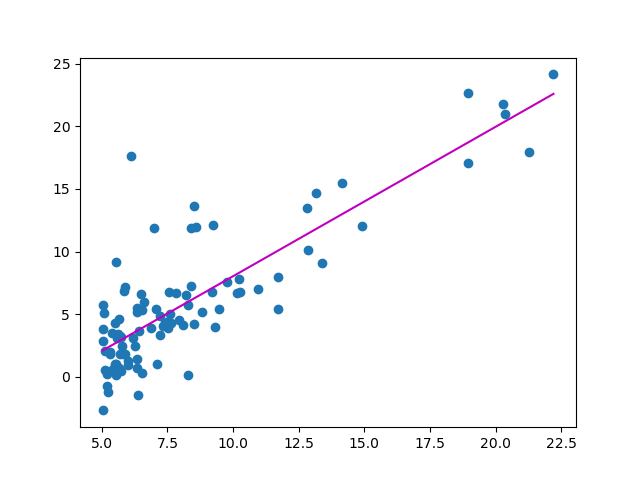
向量化:在 Python 或 Matlab 中进行科学计算时,如果有多组数据或多项式运算,转化成矩阵乘法会比直接用
for循环高效很多,可以实现同时赋值且代码更简洁。这是由于科学计算库中的函数更好地利用了硬件的特性,更好地支持了诸如循环展开、流水线、超标量等技术。