PR学习笔记 #1 KNN 分类器
本文最后更新于:2022年11月22日 晚上
该笔记是本人于哈尔滨工业大学(深圳)2021 年秋季学期「模式识别」课程的笔记,授课教师为 徐勇 教授。姑且算是一门 CV 入门课程。
PR vs. ML
「模式识别」与「机器学习」作为学校开设的人工智能领域二选一的先修课程,想必是有其考虑的。作为一个初学者,或许需要对这二者有更系统的认识。
这里引用一篇知乎回答的内容:

从上面的目录大致看出模式识别跟机器学习之间有很大部分的重叠。但是两者之间还是有很明显的区别的:
- 在模式识别中,模式即用来描述研究对象的特征。一般模式识别中的大部分分类器,都是在假定已经了用来描述对象性质的特征,系统的输入就是这些处理好的特征。因此,模式识别研究的是怎么样通过输入的特征对样本进行分类。
- 然而,如果特征与所研究的分类问题没有关系或者关系很弱,那么无论采用怎么样的分类器,都很难取得理想的分类效果。相比之下,机器学习更加关注的是特征抽取、特征分析,进而实现分类。
此外,既然上述图中还提到了「深度学习」,那不妨探讨一下经典面试题「深度学习和机器学习有什么不同?」,同样与特征有关:
- 深度学习是一种特殊的机器学习,具有强大的能力和灵活性。它通过学习将世界表示为嵌套的层次结构,每个表示都与更简单的特征相关,而抽象的表示则用于计算更抽象的表示。
- 传统的机器学习侧重人工进行特征抽取、特征分析,而深度学习从数据中先学习简单的特征,并从其逐渐学习到更为复杂抽象的深层特征,不依赖人工的特征工程。
K 近邻算法 | K-Nearest Neighbor
最近邻算法是解决分类问题的一种算法,是一种监督学习算法。它的思想是:如果一个样本点在特征空间中最相似的样本点中的属于某一个类别,则该样本也属于这个类别。
关于「相似」这个概念,涉及到样本距离的度量,常用的度量方式是二范数,对向量而言就是欧式距离(Euclidean Distance): \[ D(x,y)=\sqrt{\sum_{i=1}^n{(}x_i-y_i)^2}=\left\| x-y \right\| _2 \] 大多数情况下,欧式距离可以满足我们的需求,但有时候也需要了解其他方式:
- 闵可夫斯基距离(Minkowski Distance):\(\sqrt[p]{\sum\limits_{i=1}^{n}(|x_i-y_i|)^p}\)
- 曼哈顿距离(Manhattan Distance):\(\sum\limits_{i=1}^{n}|x_i-y_i|\),相当于 \(p=1\)
- 切比雪夫距离(Chebyshev Distance):\(\underset{i=1,\cdots ,n}{\max}\left| x_{\boldsymbol{i}}-y_i \right|\),相当于 $p=$
- 汉明距离(Hamming Distance):仅当特征值为 bool 值时使用
- 夹角余弦距离(Cosine Distance):\(\begin{aligned}\cos \theta =\frac{\sum_{i=1}^n{x_i}\times y_i}{\sqrt{\sum_{i=1}^n{x_{i}^{2}}\sum_{i=1}^n{y_{i}^{2}}}}\end{aligned}\)
算法步骤
解决了度量问题,剩下的就很简单了,假设有训练集: \[ D=\left\{x^{(i)},\;i=1,2,\cdots,m\right\},\quad C=\left\{ x^{(i)}\in \omega ^{\left( j \right)},\;j=1,2,\cdots ,N \right\} \]
- \(m\) 代表训练集中样本点的数量;
- \(x^{(i)}\) 代表第 \(i\) 个样本点,是一个 \(n\) 维向量,\(n\) 代表特征数;
- \(N\) 代表类别数,所有训练集中样本点被显式地标注。
那么,最近邻算法可以表述为:
- 计算测试样本点 \(x\) 与所有训练样本点 \(x^{(i)}\) 的距离 \(\left\| x-x^{(i)} \right\| _2\);
- 找出距离最小的情况 \(g_k\left( x \right) =\min \left\| x-x^{\left( k \right)} \right\| _2\);
- 若 \(x^{(k)}\in \omega ^{\left( j \right)}\),则测试样本 \(x \in \omega ^{\left( j \right)}\)。
然而,上述方法有明显的缺陷:单个训练样本对分类的结果有较大的影响。如果在一个样本空间中有反常的样本点,那么它很可能会影响到周围测试样本的判别。
因此,\(\text{KNN}\) 选择了多数表决法作为改进,在做决策时选择特征空间中最相似的 \(K\) 个样本点,并以其中大多数样本所属的类别作为测试样本的类别。故 \(\text{KNN}\) 算法可以改进为:
- 计算测试样本点 \(x\) 与所有训练样本点 \(x^{(i)}\) 的距离 \(\left\| x-x^{(i)} \right\| _2\);
- 找出距离最小的前 \(K\) 个样本点;
- 统计其中最多样本点所属的类别 \(\omega ^{\left( j \right)}\),则测试样本 \(x \in \omega ^{\left( j \right)}\)。
此外,\(\text{KNN}\) 算法还可以用于回归的决策,即用最近的 \(K\) 个样本的平均值作为回归预测值。
实现细节
\(\text{KNN}\) 算法是一种懒散学习法(Lazy Learing),在模型训练的过程中几乎不耗时,主要的计算量则花在预测时的计算,因此会比其他许多算法都要慢。
通过 Brute-Force 的方法找到最相近的前 \(K\) 个样本点,在样本量小、样本特征少的时候或许还能用,但实际运用中我们通常采用更高级的处理方法:
- KDTree (K-Dimension Tree):根据样本的 \(n\) 维特征建树,选取特征取值方差最大者作为根结点,将所有结点以该特征值均分为左右子树(将特征空间以超平面分割),再以同样方法递归建树。测试时,只需以测试样本点为圆心绘制超球体,在所有与球面交割的超矩形体中搜索最近邻的点。
- BallTree:KDTree 中利用球面交割矩形体的方法搜索,对于不均匀数据集,空间中的超矩形体会有许多棱角,导致会因为超球体交割于棱角导致进行多余的搜索。本方法将分割块改为超球体,建立球树以避免问题的发生,搜索回溯的方法与 KDTree 类似。
当然,上述方法在建模时需要较大的内存,属于「空间换时间」的经典样例。
超参数 K
所谓超参数(Hyper-Parameter),就是在开始模型训练之前,就人为设置好的参数,这是相对其他模型训练得出的参数(Parameter)提出的一个概念。
作为本算法唯一的参数 \(K\),就需要根据经验进行优化,以提高学习的性能和效果。下面我们通过交叉验证(Cross-Validation)来分析这个问题。
所谓的交叉验证,就是将样本数据按照一定比例,拆分出训练用的数据和验证用的数据,其中验证集不参与模型的构建。
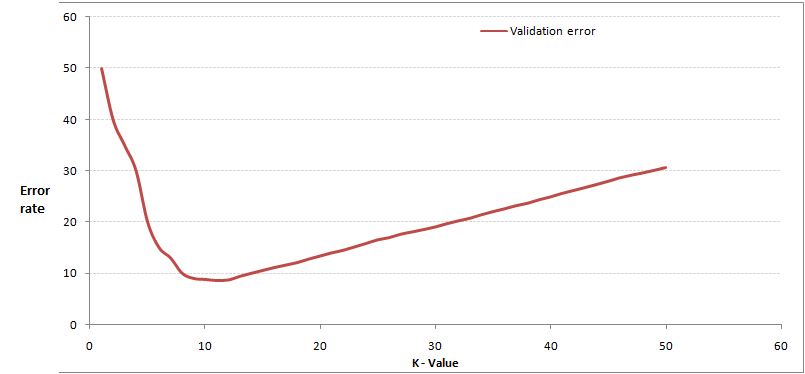
选取一个较小的 \(K\) 值,不断增加,并计算验证集的错误率,最终可以绘制出如下曲线: