ML学习笔记 #02 梯度下降:多元线性回归
本文最后更新于:2025年9月29日 凌晨
在前文 一元线性回归 的基础上,我们引入多个特征变量,探讨梯度下降对多元线性回归的解法。此外,下一节将介绍正规方程在解多元线性回归中的应用。
多元线性回归 | Multiple Linear Regression
现在我们的样本点 \(\left(x^{(i)}, y^{(i)}\right)\) 有多个特征作为输入变量,即给定的数据集为: \[ \left\{\left(x_1^{(i)},x_2^{(i)},\cdots,x_n^{(i)},y^{(i)}\right),\;i=1,2,\cdots,m\right\} \]
- \(n\) 代表单个样本的特征数量;
- \({x}^{(i)}\) 代表第 \(i\) 个观察实例的特征向量;
- \(x^{(i)}_j\) 代表第 \(i\) 个观察实例的第 \(j\) 个特征分量。
同时,回归方程 \(h\) 也具有多个参数 \(\theta_0,\theta_1,\cdots,\theta_n\): \[ h_\theta(x)=\theta_0+\theta_1x_1\cdots+\theta_nx_n \] 为简化表达式,这里假定 \(x_0 \equiv 1\) ,并以向量(vector)表示参数和自变量:\(\theta=(\theta_0,\cdots,\theta_n)^T,\;x=(x_0,\cdots,x_n)^T\),得到: \[ h_\theta(x)=\theta^Tx \]
多变量梯度下降
类似地,我们定义平方误差代价函数: \[ J(\theta)=\frac{1}{2m}\sum_{i=1}^m\left(\theta^Tx^{(i)}-y^{(i)}\right)^2 \] 我们的目标和一元线性回归中一样,要找出使得代价函数最小的一系列参数。于是, \[ \frac{\partial J}{\partial \theta}=\frac{1}{m}\sum_{i=1}^m\left(\theta^Tx^{(i)}-y^{(i)}\right)x^{(i)} \] 梯度下降时,不断作迭代: \[ \theta:=\theta-\alpha\cdot\frac{\partial J}{\partial \theta} \] 即可。
特征缩放与标准化 | Standardization
当不同自变量取值范围相差较大时,绘制的等高线图上的椭圆会变得瘦长,而梯度下降算法收敛将会很慢,因为每一步都可能会跨过这个椭圆导致振荡。这里略去数学上的证明。同理,所有依赖于「距离计算」的机器学习算法也会有此问题。
此时,我们需要把所有自变量(除了假定的 \(x_0\))进行缩放、标准化,使其落在 -1 到 1 之间。最简单的方法是,置: \[ x_i^{(j)}:=\frac{x_i^{(j)}-\mu_i}{\sigma_i} \] 其中,\(\mu_i=\frac{1}{m}\sum\limits_{j=1}^m x_i^{(j)}\) 是样本均值(Mean Value),\(\sigma_i=\sqrt{\frac{\sum\limits_{j=1}^m\left(x_i^{(j)}-\mu_i\right)^2}{m-1}}\) 是样本无偏标准差(Unbiased Standerd Deviation),就完成了标准化(Standardization)。标准化后样本均值为 0,方差为 1,但不一定是标准正态分布(与其原始分布有关),根据中心极限定理可以推出。
需要注意的是,因变量不需要标准化,否则计算的结果将失真。且如果进行了标准化,对所有待测样本点也需要进行一样的操作,参数才能生效。
此外,线性回归并不适用于所有情形,有时我们需要曲线来适应我们的数据,这时候我们也要对特征进行构造,如二次函数、三次函数、幂函数、对数函数等。构造后的新变量就可以当作一个新的特征来使用,这就是多项式回归(Polynomial Regression)。新变量的取值范围可能更大,此时,特征缩放就非常有必要!
归一化 | Normalization
人们经常会混淆标准化(Standardization)与归一化(Normalization)的概念,这里也简单提一下:归一化的目的是找到某种映射关系,将原数据固定映射到某个区间 \([a,b]\) 上,而标准化则没有限制。
归一化最常用于把有量纲数转化为无量纲数,让不同维度之间的特征在数值上有一定比较性,比如 Min-Max Normalization: \[ x_{i}^{(j)}:=\frac{x_{i}^{(j)}-\min \left( x_i \right)}{\max \left( x_i \right) -\min \left( x_i \right)} \] 又比如 Mean Normalization: \[ x_{i}^{(j)}:=x_{i}^{(j)}-\mu _i \] 但是,在机器学习中,标准化是更常用的手段,归一化的应用场景是有限的。因为「仅由极值决定」这个做法过于危险,如果样本中有一个异常大的值,则会将所有正常值挤占到很小的区间,而标准化方法则更加「弹性」,会兼顾所有样本。
学习率 \(\alpha\)
上一节谈到,学习率(Learnig rate)的选取很重要,过小则梯度下降很慢,过大则有可能不收敛。通过绘制迭代收敛曲线(Convergence Graph)可以看出学习率的好坏,也可以看出何时算法能收敛并及时终止算法。
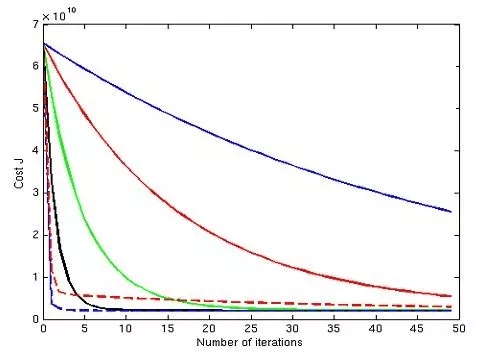
特别地,当 \(\alpha\) 取值过大时,曲线可能呈现上扬或波浪线型,解决办法都是选择更小的 \(\alpha\) 值。可以证明,只要 \(\alpha\) 足够小,凸函数都会收敛于极点。
此外,还有一种终止算法的方法:判断在某次或连续 \(n\) 次迭代后 \(J(\theta)\) 的变化小于某个极小量,如 \(\varepsilon =1e^{-3}\),此时就可以认为算法终止。但这种办法则不能用于选择尽量大的 \(\alpha\) 值。
代码实现
下面以 Coursera 上的多元线性回归数据集 ex1data2.txt 为例实现代码:
1 | |
得到的 \(\left( \theta_0, \theta_1, \theta_2 \right)\) 结果是:[340412.6595 110631.0484 -6649.4724],预测在 $( x_1=1650,x_2=3 ) $ 时的房价为 293101.0568574823。
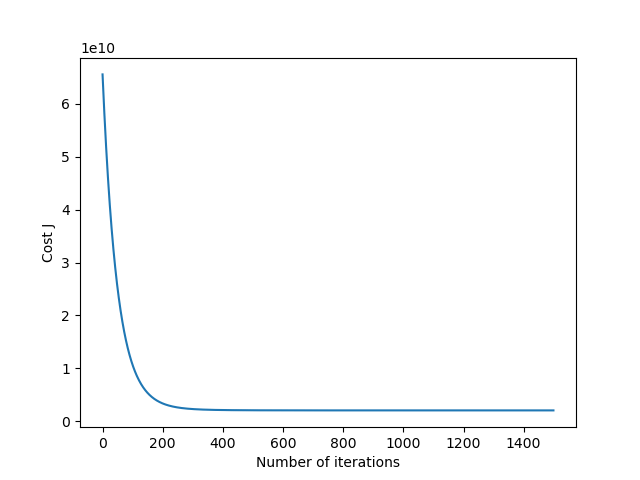
绘制的迭代收敛曲线如下: