ML学习笔记 #06 神经网络基础
本文最后更新于:2022年11月16日 中午
回顾之前学的模型,无论是线性回归还是逻辑回归都有一个缺点,即:当特征太多时,计算的负荷会非常大。而有时候,我们又希望用高次多项式来拟合更复杂的情形,此时特征数更是成倍增长。
在计算机视觉(Computer Vision)领域,数据的输入往往是一张张由像素(pixel)构成的图片。一张 \(50\times50\) 的图片中包含 \(2500\) 个像素点,如果算上 RGB 色值则有 \(7500\) 个特征,更别提包含平方、立方项特征的非线性假设了。而神经网络则是适合学习复杂的非线性假设的一类算法。
神经网络 | Neural Network
神经网络起源于科学家对人脑神经元的模拟,早期应用十分广泛,后来由于计算量过大而逐渐没落,直到近些年硬件的增强,大规模的神经网络才得以训练和应用。
神经元模型 | Neuron Model
神经网络模型建立在许多神经元之上,每个神经元也被称为激活单元(Activation unit),它采纳一些特征作为输入(input),并且根据本身的模型提供一个输出(output)。神经网络就是大量神经元相互连接形成的一个网络。
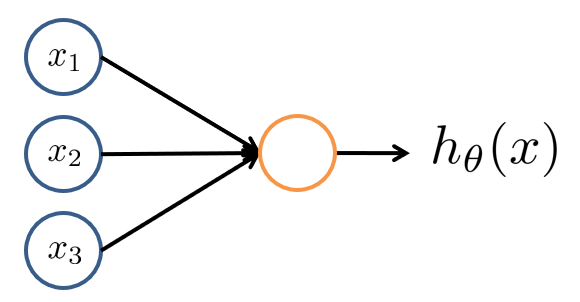
激活单元(图中黄色结点)就是一个函数,根据若干输入信息 \(x=(x_0,x_1,\cdots,x_n)^T\) 以及其权重 \(\theta=(\theta_0,\theta_1,\cdots,\theta_n)^T\),得到一个输出信息 \(h_\theta(x)\),即: \[ h_\theta(x)=f(\theta, x) \] \(h_\theta(x)\) 也称作激活函数(Activation Function),一般可以采取 \(\text{sigmoid}\) 函数 \(h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}\).
注:上图省略了 \(x_0\equiv 1\) 这一偏置项(Bias unit),偏置项不仅可以是输入层的人为特征,也可以是隐藏层的一个常量单元 \(a_0 \equiv 1\)。
为什么 \(\text{sigmoid}\) 函数可以作为激活函数?事实上激活函数有很多种,他们的共同特点都是引入了非线性假设。早期的神经网络使用 \(\text{sigmoid}\) 的原因还有:输出可映射到 Bernoulli 分布,可以作为概率解决分类问题;求导计算方便。
网络的表示 | Presentation
神经网络是许多神经元按照不同层级组织起来的网络。第一层被称作输入层(Input Layer),最后一层被称作输出层(Output Layer),中间其他层被称作隐藏层(Hidden Layer),意味着「不可见」。隐藏层和输出层具备激活函数功能,而输入层仅仅是特征的拷贝。
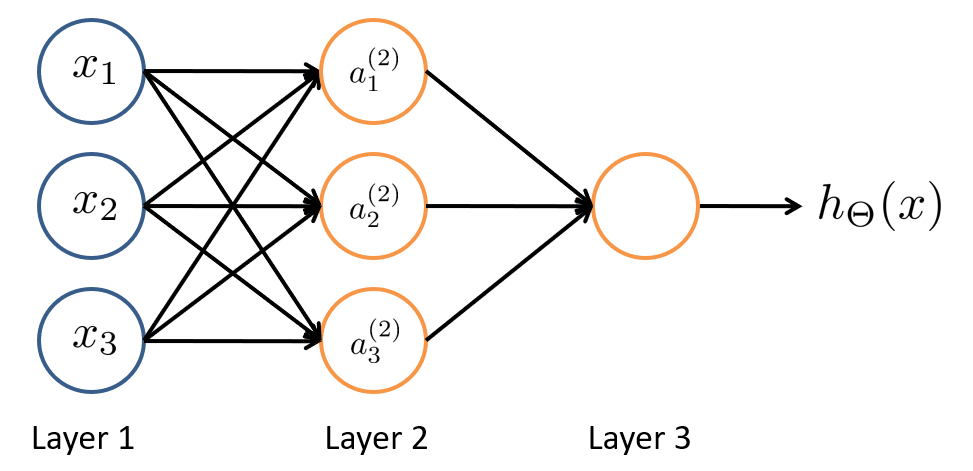
- \(x_i\) 表示输入层的第 \(i\) 个输入特征,其中 \(x_0\) 偏置项省略;
- \(a^{(j)}_i\) 表示第 \(j\) 层的第 \(i\) 个激活单元,其中 \(a_0^{(j)}\) 偏置单元省略;
- \(s_j\) 表示第 \(j\) 层的神经元数量(不包含偏置项),\(\hat a^{(j)}\in\mathbb R^{s_j+1}\) 表示加上偏置项后的 \(a^{(j)}\);
- \(\Theta^{(j)}\in\mathbb R^{s_{j+1}\times(s_j+1)}\) 表示第 \(j\) 层到第 \(j+1\) 层的权重矩阵,\(\Theta\) 表示所有权重矩阵的集合。
所以,由上图我们可以列出: \[ \begin{aligned} a_{0}^{(2)}&\equiv 1 \\ a_{1}^{(2)}&=g\left(\Theta _{10}^{(1)}+\Theta _{11}^{(1)}x_1+\Theta _{12}^{(1)}x_2+\Theta _{13}^{(1)}x_3\right) \\ a_{2}^{(2)}&=g\left(\Theta _{20}^{(1)}+\Theta _{21}^{(1)}x_1+\Theta _{22}^{(1)}x_2+\Theta _{23}^{(1)}x_3\right) \\ a_{3}^{(2)}&=g\left(\Theta _{30}^{(1)}+\Theta _{31}^{(1)}x_1+\Theta _{32}^{(1)}x_2+\Theta _{33}^{(1)}x_3\right) \\ h_{\Theta}(x)=a_{1}^{(3)}&=g\left(\Theta _{10}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)}\right) \end{aligned} \] 简写作矩阵形式,可得到前向传播(Forward Propagation)公式: \[ a^{(j+1)}=g\left(\Theta^{(j)}\hat a^{(j)}\right) \]
是不是像极了逻辑回归 \(h_\theta(x)=g\left(\theta^Tx\right)\),只不过特征 \(x\) 换成了上一层 \(\hat a^{(j)}\),假说 \(h_\theta(x)\) 变成了当前层 \(a^{(j+1)}\)。当然,由于每一层的关联性,最终的假说 \(h_{\Theta}(x)\) 依旧是特征 \(x\) 的非线性组合。
而随着每一层的深入,特征会变得越来越「抽象」,这些新特征远比单纯 \(x\) 的多项式来得强大,也能更好的预测数据。这就是神经网络相比于逻辑回归和线性回归的优势。
有的地方会把偏置项对应的偏置向量 \(b^{(j)}=\Theta_{i0}^{(j)}\in\mathbb R^{s_{j+1}}\) 单独拿出来,使得 \(\Theta^{(j)}\in\mathbb R^{s_{j+1}\times s_j}\),以求形式的统一: \[ a^{(j+1)}=g\left(\Theta^{(j)}a^{(j)}+b^{(j)}\right) \]
实现逻辑门
神经网络与逻辑门有何种联系?我们知道 \(\text{sigmoid}\) 函数具有将数值映射到 \(0\) 和 \(1\) 的能力,而逻辑门也是类似。那么就可以把逻辑门看作一个简化的二分类问题,用神经网络对其训练。通过这个例子能够直观地理解神经网络中参数的作用,首先来看最简单的与门 \(\text{AND}\):
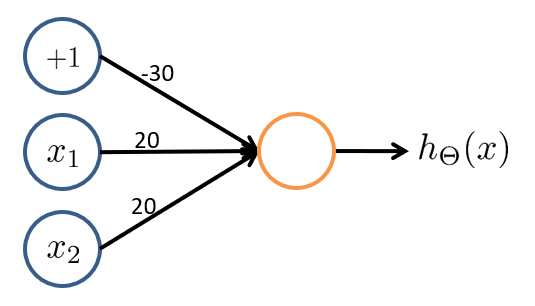
考虑一个输入层有 \(2\) 个特征且取值 \(x_1,x_2\in\{0,1\}\)、输出层有 \(1\) 个神经元且取值 \(h_\theta(x)\in\{0,1\}\) 的神经网络。如果我们将权重参数设置为:$^{(1)}=( -30,20,20 ) $,那么我们有:
| 输入 1 | 输入 2 | 输出 |
|---|---|---|
| 0 | 0 | \(g(-30)\approx 0\) |
| 0 | 1 | \(g(-10)\approx 0\) |
| 1 | 0 | \(g(-10)\approx 0\) |
| 1 | 1 | \(g(10)\approx 1\) |
这样实现了一个与门的功能,同理,或门 \(\text{OR}\)、非门 \(\text{NOT}\) 也可以用两层网络(一个激活单元)实现。但是异或门 \(\text{XOR}\) 和同或门 \(\text{XNOR}\) 则需要三层网络——由数理逻辑知,\(\text{XOR}\) 可以表示成前三者的组合 $( x_1 x_2 ) (x_1x_2 ) $,那么就可以用三个激活单元实现异或。
同时,我们也可以发现,与前三种逻辑门不同,仅用一条直线是无法画出 \(\text{XOR}\) 决策边界的:
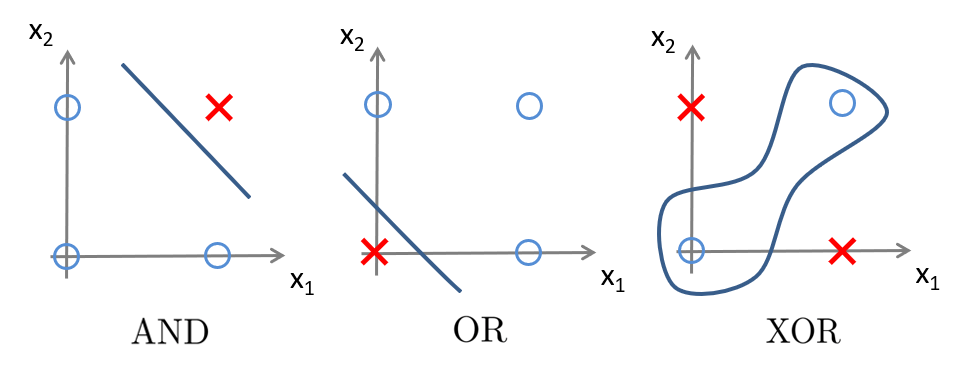
这也意味着:需要更复杂的特征(更深层的网络)来表达更高级的模型。
多分类问题
在介绍 逻辑回归 时,我们曾说对于多分类问题,可以实现多个标准的逻辑回归分类器,每个分类器的输出作为「属于某类」的概率,取其最大值作为预测结果即可。
在神经网络中,输出层的每一个神经元也可以视为一个逻辑回归分类器,对于 \(K\geqslant 3\) 个类的问题(\(K=2\) 时用一个神经元即可),最终可以得到 \(h_{\Theta}(x)\in\mathbb R^{K}\) 的预测向量,取其最大值作为预测结果即可。
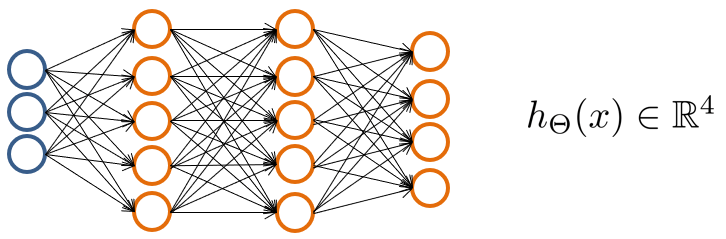
同理,在训练时也需要把标签 \(y^{\left( i \right)}\) 用独热(One-Hot)编码为向量 \(y^{\left( i \right)}=\left( 0,0,1,0 \right) ^T\) 的形式,仅有对应类的预测值为 \(1\),再通过反向传播从输出层开始计算。
代码实现
下面以 Coursera 上的多分类数据集 ex3data1.mat 为例,这是一个手写数字的数据集。本节中忽略训练过程,使用题目提供的权重参数 ex3weight.mat 作预测。
给定的数据为 .mat 格式,是 Matlab 数据二进制存储的标准格式,在 Matlab 交互窗中输入 save xxx 即可保存所有变量到 xxx.mat 文件中。Python 中使用 SciPy 的 loadmat 方法可以读入数据:
1 | |
读取的文件在 Python 中以字典存储,将其打印出来为:
1 | |
文件中一共有 \(5000\) 个样本,每个样本的输入是一个长为 \(400\) 的向量,由 \(20\times 20\) 的灰度矩阵压缩而来;输出是一个数字,表示样本图像代表的数字。
注意:为了更好地兼容 Octave/Matlab 索引(其中没有零索引),数字 \(0\) 被标记为了 \(10\),使用时可以把 \(10\) 换回成 \(0\),但题目给的
ex3weight.mat没有考虑转换;另外,数据是按列压缩的,还原回 \(20\times20\) 的矩阵后其实转置了一下,这里提前转置回去方便后续编码,但题目给的ex3weight.mat也没有考虑。
1 | |
现在我们随机挑选 \(100\) 个图像显示出来:
1 | |

下面搭建神经网络,利用已知的 \(\Theta\) 实现前向传播预测:
1 | |
调用 SciKit-Learn 库中的 metrics,生成 精度和召回率,预测结果如下:
1 | |